Курсовая работа на тему:
«Коды, исправляющие
дефекты»
Мойсеенко С. С.
Семыкина Н. А.
Декодирование помехоустойчивых кодов 4
Классификация корректирующих кодов 5
Код с постоянным весом 5
Код с четным числом единиц 6
Список
использованной литературы: 12
Введение.
История кодирования, контролирующего
ошибки, началась в 1948 г. публикацией
знаменитой статьи Клода Шеннона. Шеннон
показал, что с каждым каналом
связано измеряемое в битах в
секунду и называемое пропускной
способностью канала число С, имеющее
следующее значение. Если требуемая от
системы связи скорость передачи информации
R (измеряемая в битах в секунду) меньше
С, то, используя коды, контролирующие
ошибки, для данного канала можно построить
такую систему связи, что вероятность
ошибки на выходе будет сколь угодно мала.
В самом деле, из шенноновской
теории информации следует тот важный
вывод, что построение слишком хороших
каналов является расточительством; экономически
выгоднее использовать кодирование. В
следующем десятилетии решению этой увлекательной
задачи уделялось меньше внимания; вместо
этого исследователи кодов предприняли
длительную атаку по двум основным направлениям.
Первое направление носило
чисто алгебраический характер и
преимущественно рассматривало
блоковые коды. Первые блоковые коды были
введены в 1950 г., когда Хэмминг
описал класс блоковых кодов, исправляющих
одиночные ошибки.
Второе направление исследований
по кодированию носило скорее вероятностный
характер. Ранние исследования были связаны
с оценками вероятностей ошибки для
лучших семейств блоковых кодов, несмотря
на то, что эти лучшие коды не были
известны.
Так как развитие кодов, контролирующих
ошибки, первоначально стимулировалось
задачами связи, терминология теории кодирования
проистекает из теории связи. Построенные
коды, однако, имеют много других
приложений. Коды используются для
защиты данных в памяти вычислительных
устройств и на цифровых лентах и
дисках, а также для защиты от
неправильного функционирования или
шумов в цифровых логических цепях.
Принципы построения помехозащищенных кодов. Коды с
Составные коды. Код Грея.
В единично-десятичном коде каждая цифра десятичного числа записывается одними единицами. Например, число 325 запишется как 111 11 11111. В двоично-десятичном коде каждая цифра от 0 до 9 десятичного числа записывается четырехразрядным двоичным кодом. Такой код позволяет образовать N = 24=16 различных комбинаций. Для обозначения десяти цифр можно использовать любые 10 комбинаций из 16, поэтому возможно большое число двоично-десятичных кодов. Наибольшее применение нашел код, в котором десятичная цифра представлена ее точным двоичным числом. Такой код иногда обозначают 8—4—2—1 по весу двоичных цифр в каждом разряде. При этом цифры от 0 до 9 обозначают рядом двоичных чисел. Число 325 в двоично-десятичной системе может быть записано следующим образом: 0011—0010—0101.
Код ГРЕЯ. Код, рассматриваемый ниже носит название кода Грея и обладает тем свойством, что при переходе от любого его состояния к следующему изменяется лишь один разряд (бит), что позволяет предотвратить ошибки, поскольку в данном случае при переходе между двумя закодированными значениями все разряды никак не могут измениться одновременно. Если бы использовался чисто двоичный код, то при переходе, например, от 7 к 8 на входе можно было бы получить число 15. Для формирования состояний кода Грея существует простое правило: начинать нужно с нулевого состояния, а затем для получения, каждого следующего нужно выбрать самый младший разряд, изменение которого приводит к образованию нового состояния, и взять его инверсное значение.
Коды Грея могут содержать любое число разрядов.
Для того, чтобы избежать ошибки в случае одиночных искажений, нужно увеличить кодовое расстояние до d = 2, исключив комбинации только в одном разряде (элементе). Кодовое расстояние, обозначаемое буквой d, определяется путем сложения двух комбинаций по модулю 2 (mod 2), которое обозначается знаком + и производится в соответствии с табл.
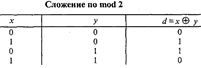
При суммировании по mod 2 двух комбинаций нули будут в тех разрядах, где символы в обеих комбинациях одинаковы, а единицы — где символы различны. Например, сложение по mod 2 двух пятиразрядных чисел дает следующий результат:
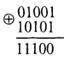
Для того, чтобы определить кодовое расстояние между различными кодовыми комбинациями, составляют матрицы
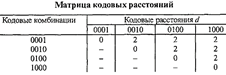
Нетрудно убедиться, что при любом одиночном искажении комбинации, приведенные в табл., не могут переходить одна в другую. Следовательно, при одиночном искажении произойдет появление новой комбинации, по которой можно судить об искажении. Двойные искажения при
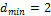
обнаружить нельзя. Для получения еще большей помехоустойчивости необходимо увеличить кодовое расстояние. Так, при
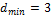
можно обнаружить любые двойные, а при
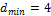
— тройные искажения. В общем случае получим выражение
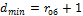
где rоб — количество ошибок, которое можно обнаружить. Для построения помехозащищенного кода необходимо разбить все комбинации на две группы: разрешенные (основные) с кодовым расстоянием
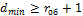
; запрещенные с кодовым расстоянием
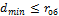
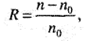
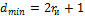
Отсюда для исправления одиночной ошибки (rи=1) dmin = 3.Способность кода обнаруживать и исправлять ошибки определяется минимальным кодовым расстоянием из выражения
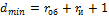
где rоб и rи — число обнаруженных и исправленных ошибок при условии
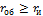
Среди помехозащищенных кодов различают блочные и непрерывные. К блочным кодам относятся такие, с помощью которых сообщения передаются блоками определенной длины из некоторого конечного числа символов. В непрерывных кодах нет последовательности информационных символов определенной длины. Между информационными символами по определенному закону размещают проверочные.
Стратегии борьбы с ошибками:
— использование корректирующих кодов или кодами с исправлением ошибок (error-correcting codes), прямое исправление ошибок FEC.
— коды с обнаружением ошибок (error-detecting codes).
Для того чтобы определить, какой метод лучше подойдет в конкретной ситуации, нужно понять, какой тип ошибок более вероятен. Ни код с исправлением ошибок, ни код с обнаружением ошибок не позволят справиться со всеми возможными ошибками, поскольку лишние биты, передаваемые для повышения надежности, также могут быть повреждены в пути.
Коды с исправлением ошибок добавляют к пересылаемой информации избыточные данные. Кадр состоит из m бит данных (то есть информационных бит) и r избыточных или контрольных бит.
Набор из n бит, содержащий информационные и контрольные биты, часто называют n-битовым кодовым словом. Кодовая норма — это часть кодового слова, несущая неизбыточную информацию, или m/n. Количество бит, которыми отличаются два кодовых слова, называется кодовым расстоянием или расстоянием между кодовыми комбинациями в смысле Хэмминга. Смысл этого числа состоит в том, что если два кодовых слова находятся на кодовом расстоянии d, то для преобразования одного кодового слова в другое понадобится d ошибок в одиночных битах.
1. Коды Хэмминга биты кодового слова нумеруются последовательно слева направо, начиная с 1. Биты с номерами, равными степеням 2 (1, 2, 4, 8, 16 и т. д.), являются контрольными. Остальные биты (3, 5, 6, 7, 9, 10 и т. д.) заполняются m битами данных.
Каждый контрольный бит обеспечивает сумму по модулю 2 или четность некоторой группы бит, включая себя самого. Один бит может входить в несколько вычислений контрольных бит. Чтобы определить, в какие группы контрольных сумм будет входить бит данных в k-й позиции, следует разложить k по степеням числа 2. Например, 11 = 8 + 2 + 1, а 29 = 16 + 8 + 4 + 1. Каждый бит проверяется только теми контрольными битами, номера которых входят в этот ряд разложения (например, 11-й бит проверяется битами 1, 2 и 8). В нашем примере контрольные биты вычисляются для проверки на четность в сообщении, представляющем букву «A» в кодах ASCII.
2. Двоичные сверточные коды не относятся к блочному типу и применяется в развернутых сетях (GSM, 802.11). Кодировщик обрабатывает последовательность входных бит и генерирует последовательность выходных бит. В отличие от блочного кода, ни- какие ограничения на размер сообщения не накладываются, также не существует грани кодирования. начение выходного бита зависит от значения текущего и предыдущих входных бит — если у кодировщика есть возможность использовать память. Число предыдущих бит, от которого зависит выход, называется длиной кодового ограничения для данного кода. Сверточные коды были очень популярны для практического применения, так как в декодировании очень легко учесть неопределенность значения бита (0 или 1). Например, предположим, что –1 В соответствует логическому уровню 0, а +1 В соот- ветствует логическому уровню 1. Мы получили для двух бит значения 0,9 В и –0,1 В. Вместо того чтобы сразу определять соответствие — 1 для первого бита и 0 для вто- рого, — можно принять 0,9 В за «очень вероятную единицу», а –0,1 В за «возможный нуль» и скорректировать всю последовательность. Для более надежного исправления ошибок к неопределенностям можно применять различные расширения алгоритма Витерби. Такой подход к обработке неопределенности значения бит называется деко- дированием с мягким принятием решений (soft-decision decoding). И наоборот, если мы решаем, какой бит равен нулю, а какой единице, до последующего исправления ошибок, то такой метод называется декодированием с жестким принятием решений (hard-decision decoding).
3. Коды Рида—Соломона (используются в сетях DSL, для исправления ошибок н DVD и Blu-ray дисках) основываются на том, что каждый многочлен n-й степени уникальным образом определяется n + 1 точкой. Например, если линия задается формулой ax + b, то восстановить ее можно по двум точкам. Коды Рида—Соломона определяются как многочлены на конечных полях. Для m-битовых символов длина кодового слова составляет 2m – 1 символов. Очень часто выбирают значение m = 8, то есть одному символу соответствует один байт. Тогда длина кодового слова — 255 байт. Широко используется код (255,233), он добавляет 32 дополнительных символа к 233 символам данных. Декодирование с исправлением ошибок выполняется при помощи алгоритма Берлекэмпа—Мэсси, который осуществляет подгонку для кодов средней длины. При добавлении 2t избыточных символов код Рида—Соломона способен исправить до t ошибок в любом из переданных символов. Это означает, например, что код (255,233) с 32 избыточными символами исправляет до 16 ошибок. Так как символы могут быть последовательными, а размер их обычно составляет 8 бит, то возможно исправление последовательных ошибок в 128 битах. Коды Рида—Соломона часто используют в сочетании с другими кодами, например сверточными. Сверточные коды эффективно обрабатывают изолированные однобитные ошибки, но с последовательностью ошибок они не справятся, особенно если ошибок в полученном потоке бит слишком много. Добавив внутрь сверточного кода код Рида—Соломона, вы сможете очистить поток бит от последовательностей ошибок.
4. Коды с малой плотностью проверок на четность (LDPC) — это линейные блочные коды, изобретенные Робертом Галлагером. В коде LDPC каждый выходной бит формируется из некоторого подмножества входных бит. Это приводит нас к матричному представлению кода с низкой плотностью единиц. Полученные кодовые слова декодируются алгоритмом аппроксимации, который последовательно улучшает наилучшее приближение, составленное из полученных данных, пока не получает допустимое кодовое слово. Так осуществляется устранение ошибок. Коды LDPC удобно применять для блоков большого размера. По этой причине коды LDPC быстро добавляются в новые протоколы. Они являются частью стандарта цифрового телевидения, сетей Ethernet 10 Гбит/с, сетей, работающих по линиям электропитания, а также последней версии 802.11.
Коды с обнаружением ошибок:
1. Код с проверкой на четность.
К отправляемым данным присоединяется бит четности (parity bit), который выбирается так, чтобы число единичных битов в кодовом слове было четным (или нечетным). Для повышения защиты от последовательностей ошибок — биты четности вычисляют не в порядке отправки данных — чередование.
Принцип обнаружения и исправления ошибок корректирующими кодами
Прежде, чем начать рассмотрение специальных корректирующих кодов, следует отметить, что любой код способен обнаруживать и исправлять ошибки, если не все кодовые слова (кодовые комбинации) этого кода используются для передачи сообщений. Нагляднее рассмотреть это на примере блочных кодов, у которых последовательность символов на выходе источника разбивается на блоки (кодовые слова, кодовые комбинации), содержащие одинаковое число символов k. При этом для двоичного кода ансамбль сообщений будет иметь объем Nр= 2 k. При помехоустойчивом кодировании это множество из Nр сообщений отображается на множество N = 2 n возможных кодовых слов, такая процедура и называется помехоустойчивым кодированием дискретных сообщений (число n – число символов в кодовом слове после кодирования,иногда его называют длиной кодовых слов или значностью кода).
В общем случае для блочного равномерного кода с основанием код имеет возможных кодовых слов. Используемые для передачи сообщений кодовые слова из множества называют разрешенными, остальные кодовые слова измножества не используются и называются запрещенными (неразрешенными для передачи).
Рисунок 89 – Обнаружение и исправление ошибок
Способ приема заключается в том, что если принятое кодовое слово принадлежит подмножеству ( i ), считается переданным -е разрешенное кодовое слово. Ошибка не может быть исправлена (исправляется неверно), если переданное кодовое слово в результате искажений превращается в кодовое слово любого другого подмножества ( j ),(j¹i). На Рисунок 48б ошибка в запрещенном кодовом слове B 1 j будет исправлена, так как это слово принадлежит подмножеству (1), приписанному к переданному разрешенному слову A 1; ошибка в кодовых словах B 2 j или B 4 j не будет исправлена, так как эти слова относятся к подмножествам, приписанным к другим разрешённым кодовым словам.
Свойства кода по обнаружению и исправлению ошибок характеризуются количественно коэффициентами обнаружения K об и исправления ошибок K ис, которые показывают, во сколько раз уменьшается вероятность ошибки после декодирования по сравнению с её величиной на входе приемного устройства (декодера), благодаря обнаружению ошибок или их исправлению соответственно. Ошибки в кодовых словах могут иметь произвольную конфигурацию, что определяется случайным характером помех в канале связи. Число ошибочных символов в принятом кодовом слове называется кратностью ошибки t, при длине кодового слова из n символов она изменяется в пределах от 0 до n.
Если это вероятность ошибки кратности t ³ 1 в n разрядном кодовом слове на входе декодера, а Pоб – вероятность обнаружения ошибок в декодере, то коэффициент обнаружения определяется следующим выражением
Коэффициент исправления ошибок будет определяться выражением
где Pис – вероятность исправления ошибок в декодере.
Последняя численно равна вероятности ошибок в кодовом слове, кратность которых не превышает величины кратности гарантированно исправляемых ошибок tис, то есть Pис = Pвх (£ tис, n).
Коэффициент исправления кода всегда меньше коэффициента обнаружения, что является общим условием для любых корректирующих кодов.
Для реализации потенциальных возможностей кода, исправляющего ошибки, необходимо учитывать статистический характер ошибок в реальных каналах связи, в которых предполагается применение этого кода. Разбиение неразрешенных комбинаций на подмножества ( i ) должно выполняться таким образом, чтобы исправлялись ошибки, появление которых наиболее вероятно в данном канале связи.
В общем случае передаваемая кодовая комбинация искажается случайным образом, что определяется случайным характером помех в канале связи. В реальных системах связи при многообразии характера действующих в линии связи помех распределение кратностей ошибок в дискретном канале связи может быть самым различным. Поэтому построению декодера, исправляющего ошибки, должно предшествовать изучение статистических свойств канала связи. В качестве примера, на Рисунок 49 приведены кривые распределения кратностей ошибок Pn (t) для двух случаев: для двоичного канала с независимыми ошибками в кодовых символах p – кривая 1 (биномиальное распределение)
Pn (t) = Cntpt (1- p) n-t (1.5)
и кривая 2 для канала, в котором передаваемое кодовое слово с одинаковой вероятностью может превратиться в другое кодовое слово данного кода (из множества N)
Pn (t) = Cnt /mn. (1.6)
Графики соответствуют длине кодового слова.
Рисунок 90 – Распределение кратностей ошибок
Для приведенных на Рисунок 48 распределений кратностей ошибок определим величины коэффициентов исправления для корректирующего кода с параметрами:, (),, исправляющего одиночные ошибки:.
Вероятность ошибки в передаваемом кодовом слове в канале с распределением кратностей ошибок Pn (t), соответствующим кривой 1(Рисунок 49), и вероятностью искажения символа кода p = 0,1 равна
Вероятность исправления ошибки (вероятность ошибки с кратностью t =1):
В канале связи с распределением кратностей ошибок Pn (t), соответствующим кривой 2 (Рисунок 49), вероятность исправления ошибки (вероятность ошибки с кратностью t =1) равна
где – доля ошибок, кратность которых ис из общего числа возможных ошибок mn. Тогда коэффициент исправления равен
Очевидно, что, если в канале связи преобладают ошибки большой кратности, целесообразно к разрешенным кодовым словам приписывать подмножество таких неразрешенных слов, которые удалены от данного разрешенного на расстояние, соответствующее этим ошибкам.
Синдромный
способ
Данный способ основан на вычислении
определенным образом контрольного числа
—синдрома ошибки. Если
синдром ошибки равен нулю, то кодовая
комбинация принята верно, если синдром
не равен нулю, то комбинация принята не
верно. Данный способ может быть использован
в кодах с исправлением ошибок, в этом
случае синдром указывает не только на
наличие ошибки в кодовой комбинации,
но и на место положение этой ошибки в
кодовой комбинации. Для двоичного кода
знание местоположения ошибки достаточно
для ее исправления. Это объясняется тем,
что любой символ кодовой комбинации может
принимать всего два значения и если символ
ошибочный, то его необходимо инвертировать.
Принципы помехоустойчивого кодирования
Помехоустойчивым (корректирующим) кодированием
называется кодирование при котором осуществляется
обнаружение либо обнаружение и исправление
ошибок в принятых кодовых комбинациях.
Возможность помехоустойчивого кодирования
осуществляется на основании теоремы,
сформулированной Шенноном, согласно
ей:
если производительность
источника меньше пропускной способности
канала связи, то существует по крайней
мере одна процедура кодирования и декодирования
при которой вероятность ошибочного декодирования
сколь угодно мала, если же производительность
источника больше пропускной способности
канала, то такой процедуры не существует.
Основным принципом помехоустойчивого
кодирования является использование
избыточных кодов, причем если для кодирования
сообщения используется простой
код, то в него специально вводят избыточность.
Необходимость избыточности объясняется
тем, что в простых кодах все
кодовые комбинации являются разрешенными, поэтому
при ошибке в любом из разрядов приведет
к появлению другой разрешенной комбинации,
и обнаружить ошибку будет не возможно.
В избыточных кодах для передачи сообщений
используется лишь часть кодовых комбинаций
(разрешенные комбинации). Прием запрещенной
кодовой комбинации означает ошибку. Причем,
в процессе приема закодированного сообщения
возможны три случая (рисунок 1).
Рисунок 1 – Случаи приема закодированного
сообщения
Прием сообщения без ошибок является
оптимальным, но он возможен только если
канал связи идеальный. В этом случае помехоустойчивое
декодирование не требуется.
В реальном канале из-за воздействия
помех происходят ошибки в принимаемых
кодовых комбинациях. Если принимаемая
кодовая комбинация в результате
воздействия помех перешла (трансформировалась)
из одной разрешенной комбинации
в другую, то определить ошибку не возможно,
даже при использовании помехоустойчивого
кодирования.
Если же передаваемая разрешенная
кодовая комбинация, в результате
воздействия помех, трансформируется
в запрещенную комбинация, то в
этом случае существует возможность
обнаружить ошибку и исправить ее.
Помехоустойчивое кодирование
может осуществляться двумя способами:
с обнаружением ошибок либо с исправлением
ошибок. Возможность кода обнаруживать
или исправлять ошибки определяется
кодовым расстоянием.
Если осуществляется кодирование
с обнаружением ошибок, то кодовое
расстояние должно быть хотя бы на единицу
больше чем кратность обнаруживаемых
ошибок, если данное условие не выполняется,
то одни из ошибок обнаруживаются, а другие
нет.
Если осуществляется кодирование
с исправлением ошибок, то кодовое
расстояние должно быть хотя бы на единицу
больше удвоенного значения кратности
исправляемых ошибок, если данное условие
не выполняется, то одни из ошибок исправляются,
а другие нет.
Классификация корректирующих
кодов
Классификация корректирующих кодов
представлена схемой (рисунок 2)
Блочные — это коды, в которых передаваемое
сообщение разбивается на блоки и каждому
блоку соответствует своя кодовая комбинация
(например, в телеграфии каждой букве соответствует
своя кодовая комбинация).
Рисунок 2 – Классификация
корректирующих кодов
Непрерывные — коды, в которых сообщение
не разбивается на блоки, а проверочные
символы располагаются между информационными.
Неразделимые — это коды, в кодовых комбинациях
которых нельзя выделить проверочные
разряды.
Разделимые — это коды, в кодовых комбинациях
которых можно указать положение проверочных
разрядов, т. е. кодовые комбинации можно
разделить на информационную и проверочную
части.
Систематические (линейные) — это коды, в которых проверочные символы
определяются как линейные комбинации
информационных символов, в таких кодах
суммирование по модулю два двух разрешенных
кодовых комбинаций также дает разрешенную
комбинацию. В несистематических кодах
эти условия не выполняются.
Декодирование помехоустойчивых
кодов
Декодирование – это процесс перехода от вторичного
отображения сообщения к первичному алфавиту.
Декодирование помехоустойчивых кодов
может осуществляться тремя способами:
способом сравнения, синдромным и мажоритарным.
Коррекция ошибок.
Исправлять ошибки труднее,
чем их детектировать или предотвращать.
Процедура коррекции ошибок предполагает
два совмещенные процесса: обнаружение
ошибки и определение места (идентификация
сообщения и позиции в сообщении). После
решения этих двух задач, исправление
тривиально – надо инвертировать значение
ошибочного бита. В наземных каналах связи,
где вероятность ошибки невелика, обычно
используется метод детектирования ошибок
и повторной пересылки фрагмента, содержащего
дефект. Для спутниковых каналов с типичными
для них большими задержками системы коррекции
ошибок становятся привлекательными.
Здесь используют коды Хэмминга или коды
свертки.
Но существуют и более
простые методы коррекции ошибок.
Например, передача блока данных, содержащего
N строк и M столбцов, снабженных битами
четности для каждой строки и столбца.
Обнаружение ошибки четности в строке
i и столбце j указывает на бит, который
должен быть инвертирован. Может показаться,
что в случае, когда неверны
два бита, находящиеся в разных
строках и столбцах, они также
могут быть исправлены. Но это не
так. Ведь нельзя разделить варианты
i1,j1 – i2,j2 и i1,j2 – i2,j1. Этот метод может быть
развит путем формирования блока данных
с N строками, M столбцами и K слоями. Здесь
биты четности формируются для всех строк
и столбцов каждого из слоев, а также битов,
имеющих одинаковые номера строк и столбцов
i,j. Полное число битов четности в этом
случае равно (N+M+1)×K +(N+1)×(M+1). Если M=N=K=8,
число бит данных составит 512, а число бит
четности – 217. Нетрудно видеть, что в этом
случае число исправляемых ошибок будет
больше 1. (Рис. 1).
Рис. 1.
Метод коррекции более одной
ошибки в блоке данных
Коды Хэмминга наиболее известные
и, вероятно, первые из самоконтролирующихся
и самокорректирующихся кодов. Построены
они применительно к двоичной системе
счисления.
Другими словами, это
алгоритм, который позволяет закодировать
какое-либо информационное сообщение
определённым образом и после
передачи (например по сети) определить
появилась ли какая-то ошибка в этом сообщении
(к примеру из-за помех) и, при возможности,
восстановить это сообщение. Опишем самый
простой алгоритм Хемминга, который может
исправлять лишь одну ошибку.
Сразу стоит сказать, что
Код Хэмминга состоит из двух частей.
Первая часть кодирует исходное сообщение,
вставляя в него в определённых местах
контрольные биты (вычисленные особым
образом). Вторая часть получает входящее
сообщение и заново вычисляет
контрольные биты (по тому же алгоритму,
что и первая часть). Если все вновь
вычисленные контрольные биты совпадают
с полученными, то сообщение получено
без ошибок. В противном случае, выводится
сообщение об ошибке и при возможности
ошибка исправляется.
Для того, чтобы понять
работу данного алгоритма, рассмотрим
пример.
Допустим, у нас есть сообщение
«habr», которое необходимо передать без
ошибок. Для этого сначала нужно наше сообщение
закодировать при помощи Кода Хэмминга.
Нам необходимо представить его в бинарном
виде.
На этом этапе стоит
определиться с, так называемой,
длиной информационного слова,
то есть длиной строки из
нулей и единиц, которые мы
будем кодировать. Допустим, у нас
длина слова будет равна 16.
Таким образом, нам необходимо
разделить наше исходное сообщение
(«habr») на блоки по 16 бит, которые мы будем
потом кодировать отдельно друг от друга.
Так как один символ занимает в памяти
8 бит, то в одно кодируемое слово помещается
ровно два ASCII символа. Итак, мы получили
две бинарные строки по 16 бит:
После этого процесс
кодирования распараллеливается, и
две части сообщения («ha» и «br»)
кодируются независимо друг от друга.
Рассмотрим, как это делается на примере
первой части.
Прежде всего, необходимо
вставить контрольные биты. Они
вставляются в строго определённых
местах — это позиции с номерами,
равными степеням двойки. В нашем
случае (при длине информационного
слова в 16 бит) это будут
позиции 1, 2, 4, 8, 16. Соответственно, у
нас получилось 5 контрольных бит
(выделенные):
Таким образом, длина
всего сообщения увеличилась
на 5 бит. До вычисления самих
контрольных бит, мы присвоили
им значение «0».
Теперь необходимо
вычислить значение каждого контрольного
бита. Значение каждого контрольного
бита зависит от значений информационных
бит, но не от всех, а только
от тех, которые этот контрольных
бит контролирует. Для того, чтобы
понять, за какие биты отвечает каждых
контрольный бит необходимо понять очень
простую закономерность: контрольный
бит с номером N контролирует все последующие
N бит через каждые N бит, начиная с позиции
N.
Здесь знаком «X»
обозначены те биты, которые контролирует
контрольный бит, номер которого
справа. То есть, к примеру, бит
номер 12 контролируется битами
с номерами 4 и 8. Ясно, что чтобы
узнать какими битами контролируется
бит с номером N надо просто
разложить N по степеням двойки.
Но как же вычислить
значение каждого контрольного
бита? Делается это очень просто:
берём каждый контрольный бит
и смотрим, сколько среди контролируемых
им битов единиц, получаем некоторое целое
число и, если оно чётное, то ставим ноль,
в противном случае ставим единицу.
Можно конечно и наоборот,
если число чётное, то ставим единицу,
в противном случае, ставим 0. Главное,
чтобы в «кодирующей» и «декодирующей»
частях алгоритм был одинаков. (Мы будем
применять первый вариант).
Высчитав контрольные биты
для нашего информационного слова получаем
следующее:
Теперь, допустим, мы получили
закодированное первой частью
алгоритма сообщение, но оно
пришло к нас с ошибкой. К примеру, мы
получили такое (11-ый бит передался неправильно):
Вся вторая часть
алгоритма заключается в том,
что необходимо заново вычислить
все контрольные биты (так же
как и в первой части) и
сравнить их с контрольными
битами, которые мы получили. Так,
посчитав контрольные биты с неправильным
11-ым битом мы получим такую картину:
Как мы видим, контрольные
биты под номерами: 1, 2, 8 не совпадают
с такими же контрольными битами,
которые мы получили. Теперь просто
сложив номера позиций неправильных
контрольных бит (1 + 2 + 8 = 11) мы получаем
позицию ошибочного бита. Теперь
просто инвертировав его и
отбросив контрольные биты, мы
получим исходное сообщение в первозданном
виде.
Метод коррекции
ошибок FEC.
Для FEC(Forward Error Correction)-кодирования
иногда используется метод сверки, который
впервые был применен в 1955 году. Главной
особенностью этого метода является сильная
зависимость кодирования от предыдущих
информационных битов и высокие требования
к объему памяти. FEC-код обычно просматривает
при декодировании 2-8 бит десятки или даже
сотни бит.
В 1967 году Эндрю Витерби (Andrew
Viterbi) разработал технику декодирования,
которая стала стандартной для кодов свертки.
Эта методика требовала меньше памяти.
Метод свертки более эффективен, когда
ошибки распределены случайным образом,
а не группируются в кластеры. Работа же
с кластерами ошибок более эффективна
при использовании алгебраического кодирования.
Одним из широко используемых
разновидностей коррекции ошибок является
турбо кодирование, разработанное
американской аэрокосмической корпорацией.
В этой схеме комбинируется два
или более относительно простых
кодов свертки. В FEC, также как
и в других методах коррекции
ошибок (коды Хэмминга, алгоритм Рида-Соломона
и др.), блоки данных из k бит снабжаются
кодами четности, которые пересылаются
вместе с данными, и обеспечивают
не только детектирование, но и исправление
ошибок. Каждый дополнительный (избыточный)
бит является сложной функцией многих
исходных информационных бит. Исходная
информация может содержаться в
выходном передаваемом коде, тогда
такой код называется систематическим,
а может и не содержаться.
Код Хэмминга
Код Хэмминга относится к классу
блочных, разделимых, систематических
кодов. Кодовое расстояние данного
кода d0=3 или d0=4.
Блочные систематические коды характеризуются
разрядностью кодовой комбинации n
и количеством информационных разрядов
в этой комбинации k остальные разряды
являются проверочными (r):
Данные коды обозначаются как (n,k).
Рассмотрим код Хэмминга (7,4). В
данном коде каждая комбинация имеет 7
разрядов, из которых 4 являются информационными,
При кодировании формируется кодовая
комбинация вида:
где аi — информационные символы;
bi — проверочные символы.
В данном коде проверочные элементы
bi находятся через линейные комбинации
информационных символов ai, причем, для каждого проверочного
символа определяется свое правило. Для
определения правил запишем таблицу синдромов
кода (таблица 1), в которой записываются
все возможные синдромы, причем, синдромы
имеющие в своем составе одну единицу
соответствуют ошибкам в проверочных
символах:
- синдром 100 соответствует ошибке в проверочном символе b1;
- синдром 010 соответствует ошибке в проверочном символе b2;
- синдром 001 соответствует ошибке в проверочном символе b3.
Синдромы с числом единиц больше
2 соответствуют ошибкам в информационных
символах. Синдромы для различных
элементов кодовой комбинации аi и bi должны быть различными.
Таблица 1 — Синдромы кода Хэмминга (7;4)
Определим правило формирования элемента
b3. Как следует из таблицы, ошибке
в данном символе соответствует единица
в младшем разряде синдрома С4. Поэтому,
из таблицы, необходимо отобрать те элементы
аi у которых, при возникновении
ошибки, появляется единица в младшем
разряде. Наличие единиц в младшем разряде,
кроме b3,соответствует элементам a1, a2 и a4. Просуммировав эти информационные
элементы получим правило формирования
проверочного символа:
b3 = a1 + a2 + a4
Аналогично определяем правила
для b2 и b1:
b2 = a1 + a3 + a4
b1 = a2 + a3 + a4
Пример 1: необходимо сформировать кодовую
комбинацию кода Хэмминга (7,4) соответствующую
информационным символам 1101.
В соответствии с проверочной матрицей
определяем bi:
b1 = 1 + 0 + 1 = 0; b2 = 1 + 0 + 1=1; b3 = 1 + 1 + 1 = 1.
Добавляем проверочные символы
к информационным и получаем кодовую
комбинацию:
Biр = 1101001.
В теории циклических кодов все
преобразования кодовых комбинаций
производятся в виде математических
операций над полиномами (степенными
функциями). Поэтому двоичные комбинации
преобразуют в полиномы согласно
выражения:
Аi(х) = 1*x6 + 0*x5 + 0*x4 + 1*x3 + 0*x2 + 1*x+1*x0 = x6 + x3 + x+1.
При формировании кодовых комбинаций
над полиномами производят операции
сложения, вычитания, умножения и
деления. Операции умножения и деления
производят по арифметическим правилам,
сложение заменяется суммированием
по модулю два, а вычитание заменяется
суммированием.
Разрешенные кодовые комбинации циклических
кодов обладают тем свойством, что
все они делятся без остатка
на образующий или порождающий полином G(х). Порождающий
полином вычисляется с применением ЭВМ.
В приложении приведена таблица синдромов.
Этапы формирования разрешенной
кодовой комбинации разделимого
циклического кода Biр(х).
1. Информационная кодовая комбинация
Ai преобразуется из двоичной формы в полиномиальную
(Ai(x)).
2. Полином Ai(x) умножается на хr,
где r количество проверочных разрядов:
3. Вычисляется остаток от деления R(x)
полученного произведения на порождающий
полином:
4. Остаток от деления (проверочные разряды)
прибавляется к информационным разрядам:
Biр(x) = Ai(x)*xr + R(x).
5. Кодовая комбинация Bip(x) преобразуется
из полиномиальной формы в двоичную (Bip).
Пример 2. Необходимо сформировать кодовую
комбинацию циклического кода (7,4) с порождающим
полиномом G(x)=х3+х+1, соответствующую информационной
комбинации 0110.
Способ
сравнения.
Этот способ основан на том, что, принятая
кодовая комбинация сравнивается со всеми
разрешенными комбинациями, которые заранее
известны на приеме. Если принятая комбинация
не совпадает ни с одной из разрешенных,
выносится решение о принятии запрещенной
комбинации. Недостатком данного способа
является громоздкость и необходимость
большого времени для декодирования в
случае применения многоразрядных кодов.
Данный способ используется в кодах с
обнаружением ошибок.
Обнаружение ошибок.
Каналы передачи данных ненадежны,
да и само оборудование обработки
информации работает со сбоями. По этой
причине важную роль приобретают
механизмы детектирования ошибок. Ведь
если ошибка обнаружена, можно осуществить
повторную передачу данных и решить
проблему. Если исходный код по своей
длине равен полученному коду,
обнаружить ошибку передачи не предоставляется
возможным.
При передаче информации она
кодируется таким образом, чтобы
с одной стороны характеризовать
ее минимальным числом символов, а
с другой – минимизировать вероятность
ошибки при декодировании получателем.
Для выбора типа кодирования важную
роль играет так называемое расстояние
Хэмминга.
Пусть А и Б две двоичные кодовые
последовательности равной длины. Расстояние
Хэмминга между двумя этими кодовыми последовательностями
равно числу символов, которыми они отличаются.
Например, расстояние Хэмминга между кодами
00111 и 10101 равно 2.
Можно показать, что для
детектирования ошибок в n битах, схема
кодирования требует применения
кодовых слов с расстоянием Хэмминга
не менее N+1. Можно также показать,
что для исправления ошибок в
N битах необходима схема кодирования
с расстоянием Хэмминга между
кодами не менее 2N+1. Таким образом, конструируя
код, мы пытаемся обеспечить расстояние
Хэмминга между возможными кодовыми
последовательностями больше, чем оно
может возникнуть из-за ошибок.
Широко распространены коды
с одиночным битом четности. В
этих кодах к каждым М бит добавляется
1 бит, значение которого определяется
четностью (или нечетностью) суммы
этих М бит. Так, например, для двухбитовых
кодов 00, 01, 10, 11 кодами с контролем четности
будут 000, 011, 101 и 110. Если в процессе передачи
один бит будет передан неверно, четность
кода из М+1 бита изменится.
Предположим, что частота
ошибок (BER) равна р=10-4. В этом случае
вероятность передачи 8 бит с ошибкой составит:
1–(1–p)8=7,9∙10-4.
Добавление бита четности
позволяет детектировать любую
ошибку в одном из переданных битах.
Здесь вероятность ошибки в одном
из 9 бит равна 9p(1–p)8. Вероятность
же реализации необнаруженной ошибки
составит: 1– (1– p)9 – 9p(1– p)8
= 3,6∙10-7.
Таким образом, добавление бита
четности уменьшает вероятность
необнаруженной ошибки почти в 1000 раз.
Использование одного бита четности
типично для асинхронного метода
передачи. В синхронных каналах чаще
используется вычисление и передача
битов четности как для строк, так и
для столбцов передаваемого массива данных.
Такая схема позволяет не только регистрировать
но и исправлять ошибки в одном из битов
переданного блока.
Контроль по четности достаточно
эффективен для выявления одиночных
и множественных ошибок в условиях,
когда они являются независимыми.
При возникновении ошибок в кластерах
бит метод контроля четности неэффективен
и тогда предпочтительнее метод
вычисления циклических сумм (CRC).
Мажоритарное
декодирование
Этот способ основано на
том, что каждый информационный символ
кодовой комбинации определяется нескольким
линейными выражениями через другие символы
кодовой комбинации. Если принята комбинация
без ошибок, то все соотношения остаются
и все выражения дают одинаковые результаты
(единицу или ноль). При ошибке в одном
из разрядов эти соотношения нарушаются,
в результате чего одни линейные выражения
равны нулю, а другие единице. Решение
о принятом символе определяется по большинству:
если в результате вычислений выражений
больше нулей, то принимается решение
о принятии нуля, если больше единиц, то
принимается решение о приеме единицы.
Если, при декодировании, результаты вычисления
выражений дают одинаковое число единиц
и нулей, то при определении принятого
символа приоритет имеет принятый символ,
значение которого в данный момент определяется.
Код с четным числом единиц
Данный код относится к классу
блочных, разделимых, систематических
кодов. В нем все разрешенные
кодовые комбинации имеют четное
число единиц. Это достигается
введением в кодовую комбинацию
одного проверочного символа, который
равен единице если количество единиц
в информационной комбинации нечетное
и нулю, если четное. Например:
При декодировании осуществляется
поразрядное суммирование по модулю
два всех элементов принятой кодовой
комбинации и если результат равен
единице, то принята комбинация с
ошибкой, если результат равен нулю,
то принята разрешенная комбинация. Например:
101101 = 1 + 0 + 1 + 1 + 0 + 1 = 0 — разрешенная
комбинация
101111 = 1 + 0 + 1 + 1 + 1 + 1 = 1 — запрещенная
комбинация.
Данный код способен обнаруживать
как однократные ошибки, так и
любые ошибки нечетной кратности, но
не способен их исправлять. Данный код
также используется в системах передачи
информации с обратной связью.
Код с постоянным весом
Данный код относится к классу
блочных не разделимых кодов. В нем
все разрешенные кодовые комбинации
имеют одинаковый вес. Примером кода
с постоянным весом является Международный
телеграфный код МТК-3. В этом коде
все разрешенные кодовые комбинации
имеют вес равный трем, разрядность
же комбинаций n=7. Таким образом, из
128 комбинаций (N0 = 27 = 128) разрешенными являются
Nа = 35 (именно столько комбинаций из всех
имеют W=3). При декодировании кодовых комбинаций
осуществляется вычисление веса кодовой
комбинации и если W≠3, то выносится решение
об ошибке. Например, из принятых комбинаций
0110010, 1010010, 1000111 ошибочной является третья,
т. к. W=4. Данный код способен обнаруживать
все ошибки нечетной кратности и часть
ошибок четной кратности. Не обнаруживаются
только ошибки смещения, при
которых вес комбинации не изменяется,
например, передавалась комбинация 1001001,
а принята 1010001 (вес комбинации не изменился
W=3). Код МТК-3 способен только обнаруживать
ошибки и не способен их исправлять. При
обнаружении ошибки кодовая комбинация
не используется для дальнейшей обработки,
а на передающую сторону отправляется
запрос о повторной передаче данной комбинации.
Поэтому данный код используется в системах
передачи информации с обратной связью.
