Всем привет! Сегодня я хочу рассказать вам немного о коде Хэмминга (7; 4). Этот простейший код может быть с лёгкостью применён любым человеком для передачи самокорректирующихся сообщений , и сегодня я хочу вам показать как именно этот код можно легко и просто использовать.
Структурно слова кода Хэмминга состоят из двух частей. Сначала идут информационные 4 бита, затем три бита проверочных. Будем обозначать информационные биты буквами ABCD, проверочные буквами xyz.
Таким образом слово кода Хэмминга имеет следующую структуру:
Для передачи 4 бит информации нам требуется передавать кодовое слово из целых 7 бит! Последние три бита в случае, когда ошибки отсутствуют, не несут никакой новой информации, ибо они зависят от первых 4. Однако если в кодовом слове из 7 бит произошла 1 ошибка, то исходные информационные 4 бита всё равно можно будет восстановить точно! В этом и состоит главная особенность самокорректирующихся кодов.
Естественно, использование кода Хэмминга при передаче данных требует увеличенных ресурсов. Здесь есть такое важное понятие как скорость кода — отношение числа информационных бит к общему числу бит. В случае кода Хэмминга скорость равна 4/7. , к примеру, чтобы передавать информацию со скоростью 1 Мбит/сек и коррекцией ошибок с помощью кода Хэмминга вам потребуется канал с пропускной способностью минимум в 7/4=1. 75 Мбит/сек.
Для подсчёта проверочных бит можно использовать следующие формулы:
где n mod 2 означает остаток от деления числа n на 2.
К примеру, если информационный вектор есть ABCD = 1001, то кодовый вектор будет ABCDxyz = 1001 100
Вместо непонятных формул можно использовать следующую картинку:
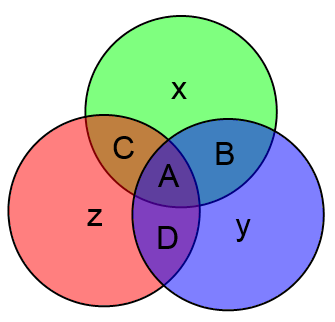
Здесь всё очень просто. Подставляете вместо букв значения соответствующих битов и затем считаете значения x, y и z как сумму по модулю 2 тех информационных бит, которые есть в соответствующем круге.
В приведённом выше примере будет:
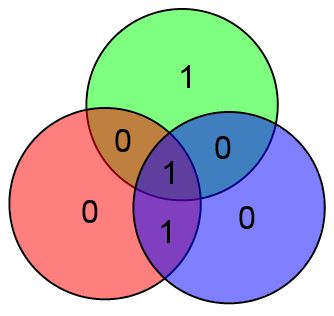
Куда более интересным является вопрос об исправлении ошибок. Очевидно, вывод об отсутствии ошибок приёмник может сделать просто взяв информационные биты ABCD, посчитав на их основе проверочные биты xyz и сравнить посчитанные проверочные биты с принятыми. Если есть ошибка, то часть проверочных битов не совпадёт.
Предположим что произошла ошибка в проверочном бите y и было принято слово 1001 110
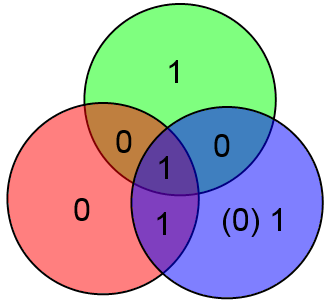
В таком случае два проверочных бита сойдутся, а один нет. Этого вполне достаточно чтобы сделать вывод что нужно исправить бит y (для которого проверка не сошлась).
Предположим, что произошла ошибка в одном из информационных битов BCD — к примеру в бите B.
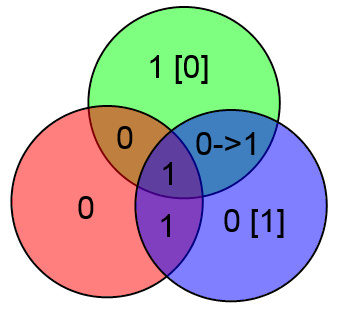
В таком случае не сойдутся аж два проверочных бита — x (он равен 1, а “должен” равняться 0) и y. Посмотрев на круги легко увидим что они пересекаются по битам B и A. не сошлось две проверки, то берём бит B (расположенный на пересечении двух проверок).
Наконец, отдельно рассмотрим бит A. Если в нём ошибка, то у нас не сойдутся все три проверки:
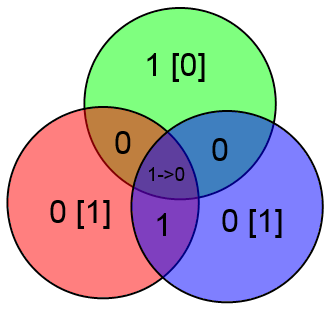
Увидев такое безобразие сразу же делаем вывод о том, что ошибка в бите A.
Таким образом, можно легко и просто вычислять локацию ошибки и исправлять её. Замечу что если ошибок больше одной, то описанный выше алгоритм сработает неверно. К примеру, допустим что произошли ошибки в битах C и z:
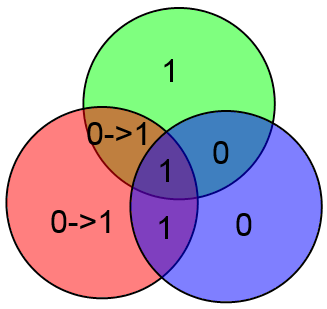
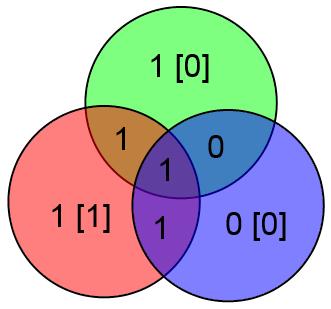
Проверочные биты y и z сойдутся, а бит x нет. Алгоритм исправит бит x и всё. Это вполне естественное поведение, т. если вероятность ошибки p < 1, то вероятность двух ошибок меньше чем вероятность одной ошибки (p^2 < p <= p < 1 при p <> 0).
Естественно, работать с цветными кругами удобно человеку, но неудобно компьютеру. У кодов Хэмминга есть одна особенность, которая позволяет их лёгкое декодирование на компьютере. Итак, рассмотрим следующий алгоритм:
Определим числа g, b, r как сумму всех четырёх бит в кругах соответствующего цвета
Фактически каждый из этих бит можно определить как сумму соответствующего проверочного бита, вычисленного на основании принятых информационных бит, с принятым проверочным битом. к примеру g есть сумма (A + B + C mod 2) (по этой формуле считался x на стороне передатчика) и принятого x. Аналогично b соответствует y, r соответствует z.
Если же есть 1 ошибка, то число gbr есть номер (в двоичной записи) ошибочного бита в векторе ABCxDyz.
В качестве примера рассмотрим уже знакомый нам вектор ABCDxyz = 1001 100, в котором произошла ошибка в бите x (четвёртый бит в векторе ABCxDyz). Посчитаем gbr:
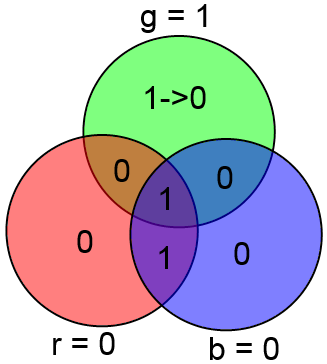
На этом всё, спасибо за внимание!
Пропускная способность любого реального канала связи огранича. Это значит, что есть некоторая наибольшая возможная скорость передачи данных, которую принципиально невозможо превысить.
Основная единица измерения скорости — биты в секунду (бит/с, англ. bps — bits per second). Для характеристики быстродействующих каналов применяют килобиты в секунду (Кбит/с) и мегабиты в секунду (Мбит/с), иногда используют байты в секунду (байт/с) и килобайты в секунду (Кбайт/с).
Информационный объём I данных, переданных по каналу за время t , вычисляется по формуле I = v • t, где v — скорость передачи данных. Например, если скорость передачи данных равна 512 000 бит/с, за 1 минуту можно передать файл объёмом
512 000 бит/с • 60 с = 30 720 000 битов = 3 840 000 байтов = 3075 Кбайт.
В реальных каналах связи всегда присутствуют помехи, искажающие сигнал. В некоторых случаях ошибки допустимы, например, при прослушивании радиопередачи через Интернет небольшое искажение звука не мешает понимать речь. Однако чаще всего требуется обеспечить точную передачу данных. Для этого в первую очередь нужно определить факт возникновения ошибки и, если это произошло, передать блок данных ещё раз.
Представьте себе, что получена цепочка нулей и единиц 1010101110, причём все биты независимы. В этом случае нет абсолютно никакой возможности определить, верно ли передана последовательность. Поэтому необходимо вводить избыточность в передаваемое сообщение (включать в него «лишние» биты) только для того, чтобы обнаружить ошибку.
Простейший вариант — добавить 1 бит в конце блока данных, который будет равен 1, если в основном сообщении нечётное число единиц, и равен 0 для сообщения с чётным числом единиц. Этот дополнительный бит называется битом чётности. Бит чётности используется при передаче данных в сетях, проверка чётности часто реализуется аппаратно (с помощью электроники).
Например, пусть требуется передать два бита данных. Возможны всего 4 разных сообщения: 00, 01, 10 и 11. Первое и четвёртое из них содержат чётное число единиц (0 и 2), значит, бит чётности для них равен 0. Во втором и третьем сообщениях нечётное число единиц (1), поэтому бит чётности будет равен 1. Таким образом, сообщения с добавленным битом чётности будут выглядеть так:
000, 011, 101, 110.
Первые два бита несут полезную информацию, а третий (подчёркнутый) — вспомогательный, он служит только для обнаружения ошибки. Обратим внимание, что каждое из этих трёхбитных сообщений содержит чётное число единиц.
Подумаем, сколько ошибок может обнаружить такой метод. Если при передаче неверно передан только один из битов, количество единиц в сообщении стало нечётным, это и служит признаком ошибки при передаче. Однако исправить ошибку нельзя, потому что непонятно, в каком именно разряде она случилась.
Если же изменилось два бита, чётность не меняется, и такая ошибка не обнаруживается. В длинной цепочке применение бита чётности позволяет обнаруживать нечётное число ошибок (1, 3, 5,. ), а ошибки в чётном количестве разрядов остаются незамеченными.
Контроль с помощью бита чётности применяется для небольших блоков данных (чаще всего — для каждого отдельного байта) и хорошо работает тогда, когда отдельные ошибки при передаче независимы одна от другой и встречаются редко.
Для обнаружения искажений в передаче файлов, когда может сразу возникнуть множество ошибок, используют другой метод — вычисляют контрольную сумму с помощью какой-нибудь хэш-функции (вспомните материал учебника для 10 класса). Чаще всего для этой цели применяют алгоритмы CRC (англ. Cyclic Redundancy Code — циклический избыточный код), а также криптографические хэш-функции MD5, SHA-1 и другие. Если контрольная сумма блока данных, вычисленная приёмником, не совпадает с контрольной суммой, записанной передающей стороной, то произошла ошибка.
Помехоустойчивые коды.
Значительно сложнее исправить ошибку сразу (без повторной передачи), однако в некоторых случаях и эту задачу удаётся решить. Для этого требуется настолько увеличить избыточность кода (добавить «лишние» биты), что небольшое число ошибок всё равно позволяет достаточно уверенно распознать переданное сообщение. Например, несмотря на помехи в телефонной линии, обычно мы легко понимаем собеседника. Это значит, что речь обладает достаточно большой избыточностью, и это позволяет исправлять ошибки «на ходу».
Пусть, например, нужно передать один бит, 0 или 1. Утроим его, добавив ещё два бита, совпадающих с первым. Таким образом, получаются два «правильных» сообщения:
000 и 111.
Теперь посмотрим, что получится, если при передаче одного из битов сообщения 000 произодёт ошибка и приёмник получит искажённое сообщение 001. Заметим, что оно отличается одним битом от 000 и двумя битами от второго возможного варианта — 111. Значит, скорее всего, произошла ошибка в последнем бите и сообщение нужно исправить на 000. Если приёмник получил 101, можно точно сказать, что произошла ошибка, однако попытка исправить её приведёт к неверному варианту, так как ближайшая «правильная» последовательность — это 111. Таким образом, такой код обнаруживает одну или две ошибки. Кроме того, он позволяет исправить (!) одну ошибку, т. является помехоустойчивым.
Помехоустойчивый код — это код, который позволяет исправлять ошибки, если их количество не превышает некоторого уровня.
Выше мы фактически применили понятие «расстояния» между двумя кодами. В теории передачи информации эта величина называется расстоянием Хэмминга в честь американского математика Р. Хэмминга.
Расстояние Хэмминга — это количество позиций, в которых различаются два закодированных сообщения одинаковой длины.
Например, расстояние d между кодами 001 и 100 равно
потому что они различаются в двух битах (эти биты подчёркнуты). В приведённом выше примере расстояние между «правильными» последовательностями (словами) равно d(000, 111) = 3. Такой код позволяет обнаружить одну или две ошибки и исправить одну ошибку.
В общем случае, если минимальное расстояние между «правильными» словами равно d, можно обнаружить от 1 до d – 1 ошибок, потому что при этом полученный код будет отличаться от всех допустимых вариантов. Для исправления r ошибок необходимо, чтобы выполнялось условие
d ≥ 2r +1.
Это значит, что слово, в котором сделано r ошибок, должно быть ближе к исходному слову (из которого оно получено искажением), чем к любому другому.
Рассмотрим более сложный пример. Пусть нужно передавать три произвольных бита, обеспечив обнаружение двух любых ошибок и исправление одной ошибки. В этом случае можно использовать, например, такой код с тремя контрольными битами (они подчеркнуты);
011 100 111 001
Расстояние Хэмминга между любыми двумя словами в таблице не менее 3, поэтому код обнаруживает две ошибки и позволяет исправить одну. Как же вычислить ошибочный бит?
Предположим, что было получено кодовое слово 011011. Определив расстояние Хэмминга до каждого из «правильных» слов, находим единственное слово 010011, расстояние до которого равно 1 (расстояния до остальных слов больше). Значит, скорее всего, это слово и было передано, но исказилось из-за помех.
На практике используют несколько более сложные коды, которые называются кодами Хэмминга. В них информационные и контрольные биты перемешаны, и за счёт этого можно сразу, без перебора, определить номер бита, в котором произошла ошибка. Наиболее известен семибитный код, в котором 4 бита — это данные, а 3 бита — контрольные. В нём минимальное расстояние между словами равно 3, поэтому он позволяет обнаружить две ошибки и исправить одну.
Вопросы и задания
В каких единицах измеряют скорость передачи данных?
Почему для любого канала связи скорость передачи данных ограничена?
Как вычисляется информационный объем данных, который можно передать за некоторое время?
В каких случаях при передаче данных допустимы незначительные ошибки?
Что такое избыточность сообщения? Для чего её можно использовать? Приведите примеры.
Как помехи влияют на передачу данных?
Что такое бит чётности? В каких случаях с помощью бита чётности можно обнаружить ошибку, а в каких – нельзя?
Можно ли исправить ошибку, обнаружив неверное значение бита четности?
Для чего используется метод вычисления контрольной суммы?
Какой код называют помехоустойчивым?
Каково должно быть расстояние Хэмминга между двумя любыми кодами, чтобы можно было исправить две ошибки?
Как исправляется ошибка при использовании помехоустойчивого кода?
Сколько ошибок обнаруживает 7-битный код Хэмминга, описанный в конце параграфа, и сколько ошибок он позволяет исправить?
а) «Алгоритмы CRC»
б) «Коды Хемминга»
Вернуться в главу
Вопросы и задания
В каких единицах измеряют скорость передачи данных?
2. Почему для любого канала связи скорость передачи данных ограничена?
3. Как вычисляется информационный объём данных, который можно передать за некоторое время?
4. В каких случаях при передаче данных допустимы незначительные ошибки?
5. Что такое избыточность сообщения? Для чего её можно использовать? Приведите примеры. Как помехи влияют на передачу данных?
7. Что такое бит чётности? В каких случаях с помощью бита чётности можно обнаружить ошибку, а в каких — нельзя?
8. Можно ли исправить ошибку, обнаружив неверное значение бита чётности?
9. Для чего используется метод вычисления контрольной суммы?
10. Какой код называют помехоустойчивым?
11. Каково должно быть расстояние Хэмминга между двумя любыми кодами, чтобы можно было исправить 2 ошибки?
12. Как исправляется ошибка при использовании помехоустойчивого кода?
13. Сколько ошибок обнаруживает 7-битный код Хэмминга, описанный в конце параграфа, и сколько ошибок он позволяет исправить?
а) «Алгоритмы CRC»
б) «Коды Хемминга»
Следующая страница Задачи
Cкачать материалы урока
