Таблица 2
Простой четырех символьный код C(x) Образующий полином P(x) Циклический (7,4) код 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 11111101 0000000 0001101 0011010 0010111 0110100 0111001 0101110 0100011 1101000 1100101 1110010 1111111 1011100 1010001 1000110 1001011
Способы исправления ошибок на основе синдрома ошибок, свойства цикличности и анализ веса остатка
Синдром циклического кода, как и в любом систематическом коде, определяется суммой по модулю два, принятых проверочных элементов и элементов первичной группы, сформированных из принятых элементов информационной группы.
В циклическом коде для определения синдрома следует разделить приятую кодовую комбинацию на кодовую комбинацию производящего полинома. Если все элементы приняты без ошибок, остаток R(x) от деления равен нулю. Наличие ошибок приводит к тому, что остаток R(x)≠0.
Для определения номеров элементов, в которых произошла ошибка, существует несколько методов. Один из них основан на свойстве, которое заключается в том, что R(х), полученный при делении принятого многочлена H(x) на Pr(x), равен R(x), полученному в результате деления соответствующего многочлена ошибок E(x) на Pr(x).
Элемент с ошибкой a1 a2 a3 a4 a5 Синдром 0101 1011 1100 0110 0011
Указанное однозначное соответствие можно использовать для определения места ошибки. Синдром не зависит от переданной кодовой комбинации, но в нем сосредоточена вся информация о наличии ошибок. Обнаружение и исправление ошибок в систематических кодах может производиться только на основе анализа синдрома.
На основании приведенного свойства существует следующий метод определения места ошибки. Сначала определяется остаток R1(0,1), соответствующий наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде (более низком), то такой же остаток получится в произведении принятого многочлена и x, т. H(x)x. Это служит основанием для следующего приема, суть которого ясна из следующего примера.
Пример: Предположим, задан код (11,7) в виде кодовой комбинации 10110111100. Здесь последние четыре разряда проверочные и получены на основе использования производящего многочлена P(0,1)=100011. Принята кодовая комбинация 10111111100. Определить ошибочно принятый элемент.
Вычисляем R(x) как остаток от деления E(x)=10000000000 на 10011. Произведя деление, получим 0111. Далее делим принятую комбинацию на Pr(x) и получаем остаток R(0,1). Если R(0,1)=R1(0,1), то ошибка в старшем разряде. Если нет, то дописываем «0» и продолжаем деление. Номер ошибочно принятого разряда (отсчет слева направо) на единицу больше числа приписанных нулей, после которых остаток окажется равным 0111. Проведем процесс деления, отмечая штрихом получаемые остатки R1(0,1), R2(0,1), R3(0,1), R4(0,1):

В данном примере для этого пришлось дописать четыре нуля. Это означает, что ошибка произошла в пятом элементе, т. исправленная кодовая комбинация будет имееть вид

На основе свойства цикличности, предполагается, что ошибка произошла в старшем разряде. Определяется остаток, соответствующий вектору ошибок:


если остатки совпадают, то ошибка произошла в старшем разряде; если не совпадают, то дописывается 0 в комбинацию R(x) и продолжается деление, пока остатки не совпадут.
Важным свойством циклических кодов является то, что все они строятся с помощью образующего полинома Р(х). приведем методику построения циклического кода. Образующий полином Р(х) принимает участие в образовании каждой кодовой комбинации, поэтому комбинация кода делится на образующий полином без остатка. Однако без остатка делятся только те многочлены (комбинации), которые принадлежат данному коду, т. образующий полином позволяет выбрать разрешенные кодовые комбинации из всех возможных. Если же при делении принятой кодовой комбинации циклического кода на образующий многочлен будет получен остаток, значит, имеет место ошибка. Таким образом, остатки от деления принятой комбинации на образующий полином являются опознавателями ошибок циклических кодов. Но данные остатки еще не указывают непосредственно на место ошибки в кодовой комбинации.
В циклических кодах идея исправления ошибок основывается на следующем: ошибочная комбинация после переделанного числа циклических сдвигов «подгоняется» под остаток таким образом, чтобы в сумме с остатком она давала бы исправленную комбинацию. Остаток при этом представляет собой разницу между искаженными и правильными символами, а единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами комбинациями. «Подгоняют» искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть равно числу ошибок tи, исправляемых данным кодом (код исправляет три ошибки и в искаженной комбинации три ошибки) или меньше tи (код исправляет три ошибки, в принятой комбинации – одна ошибка).
Таким образом, для обнаружения и исправления ошибочного разряда производят следующие операции.
1) Принятую комбинацию делят на образующий полином;
2) Подсчитывают количество единиц в остатке (вес остатка). Если

где tи – допустимое число исправляемых данным кодом ошибок, принятую комбинацию складывают по модулю два с получением остатком. Сумма дает исправленную комбинацию. Если

3) Производят циклический сдвиг принятой комбинации влево на один разряд. Комбинацию, полученную в результате циклического сдвига, делят на образующий полином Р(х). В результате повторного деления
4) Производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делимого с последним остатком. Полученная комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес
5) Повторяют операцию из пункта 3 до тех пор, пока не будет достигнуто
В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатком от деления этой комбинации на образующий многочлен, а затем
6) Производят циклический сдвиг вправо ровно на столько разрядов, на сколько сдвинута суммируемая с последним остатком комбинация относительно принятой комбинации. В результате получим исправленную комбинацию.
Пример. При передаче комбинации 1001110 циклического кода, исправляющего одиночные ошибки (tи=1), полученного с помощью образующего полинома

произошла ошибка в четвертом разряде. Принятая комбинация имеет вид 1000110. Процесс исправления ошибки следующий:
Делим принятую комбинацию на образующий полином:

Сравниваем вес полученного остатка w с числом исправляемых ошибок tи=1, т.
Производим циклический сдвиг принятой комбинации на один разряд влево и деление на P(x):

Повторяем п. 3 до тех пор, пока небудет получено

Складываем по модулю два последнее делимое с последним остатком:

Производим циклический сдвиг комбинации, полученный в результате суммирования последнего делимого с последним остатком, вправо на четыре разряда (так как перед этим мы четырежды сдвигали принятую комбинацию влево):

Как видим, последняя комбинация соответствует переданной, т. не содержит ошибки.
Помехоустойчивые коды для коррекции независимых ошибок
Код Голея занимает уникальное и важное место в теории кодирования. В силу такой хорошей сфере не удивительно, что код Голея тесно связан со многими математическими объектами, и поэтому его можно использовать для перехода от изучения теории кодирования к глубоким задачам теории групп и других областей математики. Дело в том, что код Голея относится к классу совершенных кодов, для которых выполняется следующее условие:
где n – количество разрядов в кодовой комбинации
k – количество информационных разрядов в кодовой комбинации
Определим код Голея как двоичный циклический код через его порождающий многочлен.
Пусть g(x) и g(x) следующие взаимные многочлены:
g(x)= x11 +х10+х6+х5+х4+х2+1 (3
Простым вычислением проверяется, что
так что в качестве порождающего многочлена циклического (23,12)-кода можно использовать g(x), так и g(x). Как было сказано выше, минимальное расстояние кода не может быть больше 7. Ниже перечисленные утверждения совместно означают, что минимальный вес кода равен, по меньшей мере, 7.
в коде нет слов веса 4 или меньше;
в коде нет слов веса 2, 6, 10, 14, 18 и 22;
в коде нет слов веса 1, 5, 9, 13. 17 и 21.
Все веса слов в коде Голея исчерпываются числами: 0, 7, 8, 11, 12, 15, 16 и 23. Просчитанное на ЭВМ число слов каждого веса приведено в таблице 3.
Для кодирования используются три разновидности кода Голея:
• стандартный код Голея с параметрами (23, 12, 7);
• расширенный – (24, 12, 8);
• укороченный – (18, 6, 8).
Расширенный код Голея (24, 12, 8) образовался добавлением к стандартному одного бита контроля четности. Укороченный код (18, 6, 8) получается путем вычитания левых наибольших шести битов из расширенного кода.
Веса слов кода Голея
ВесЧисло слов(23,12)-код(24,12)-код 0 11 7 253- 759 8 506 11 12882576 12 1288 15 506 759 16 253 23 1 024-14096 4096
Длина вектора ошибок равна 23, а вес не превосходит 3. Длина синдромного регистра равна 11. Если данная конфигурация ошибок не вылавливается, то она не может быть циклически сдвинута так, чтобы все три ошибки появились в 11 младших разрядах. Можно убедиться, что в этом случае по одну сторону от одной из трех ошибочных позиций стоит, по меньшей мере, пять, а по другую сторону – по меньшей мере, шесть нулей. Следовательно, каждая исправляемая конфигурация ошибок может быть с помощью циклических сдвигов приведена к одному из трех следующих видов (позиции нумеруются числами от 0 до 22):
все ошибки (не более трех) расположены в 11 старших разрядах;
одна ошибка занимает пятую позицию, а остальные расположены в 11 старших разрядах;
одна ошибка занимает шестую позицию, а остальные расположены в 11 старших разрядах. Таким образом, в декодере надо заранее вычислить величины:
Тогда ошибка вылавливается, если вес S(x) не превышает 3 или вес S(x)-Ss(x) либо S(x)-Se(x) не превышает 2. В декодере можно исправлять все три ошибки, если эти условия выполнены, либо исправлять только две ошибки в младших 11 битах, дожидаясь удаления из регистра третьего ошибочного бита. Разделив х16 и х17 на образующий полином g(x)=x11+х10+х6+х5+х4+х2+1, получаем: S5(x)=x9+x8+x6+x4+x2+x
(в двоичной форме 01100110110) S6(x)=x10+x9+x7+x6+x3+x2
(в двоичной форме 00110011011)
Следовательно, если ошибка содержится в пятой или шестой позициях, то синдром соответственно равен (01100110110) или (00110011011). Наличие двух дополнительных ошибок в 11 старших разрядах приводит к тому, что в соответствующих позициях два из этих битов заменяются на противоположные.
Принцип кодирования и декодирования кода Голея
Так как код Голея является разновидностью циклических кодов, то к нему применимы следующие методы кодирования:
1-й метод: Деление на образующий полином g(х)
xr (x) R(x)
———- = Q(x) + ———- (3
Видоизменив уравнение, получим:
Q(x)g(x) = xr (x) + R(x), (3
где (х) – кодовая комбинация,
r – степень образующего полинома.
Данный метод кодирования основан на следующем:
кодовую комбинацию а=(а0, a1,. , аk-1) сдвигаем па хr разрядов влево (сдвиг аналогичен умножению на хr);
полученную в результате сдвига комбинацию a=(аk-1,. , аn-1), делим на образующий полином g(x);
полученный остаток от деления R(x) размещаем на позициях (а0,,. , аn-1) кодовой комбинации.
Для кодирования комбинации (110101101101), которой соответствует многочлен
(х)= x11 +х10+х8+х6+х5+х3+ х2+1, умножим сначала на х11 , а затем разделим хr (х) на образующий полином g(x) и найдем остаток R(x). В результате деления находим, что
R(x)= x10+х9+х8+х6+х5+х4+ х3+x2. Кодовый многочлен образуется путем сложения хг(х) и R(x) согласно (2.
Этому многочлену соответствует комбинация циклического кода, в которой
Информационная часть Проверочная часть
2-й метод: Умножение на образующий полином g(x)
F(x) ≤ p(x)g(x) (3
Данный метод основан на умножении кодовой комбинации (х) на образующий полином g(x). В результате получается комбинация несистематического кода, т. комбинация, в которой нельзя определить информационные и проверочные разряды.
Необходимо умножить многочлен (x)= x11 +х10+х8+х6+х5+х3+ х2+1 на g(x)=x11+x9+x7+x6+x5+x+1. Умножение осуществляется с использованием сложения по модулю 2. В результате получаем:
Этому многочлену соответствует комбинация циклического кода:
3-й метод: Использование производящей и проверочной матриц. Этот метод основан на использовании производящей g(x) и проверочной Н(х) матриц.
Как и всякий линейный код, циклический код задается парой матриц: производящей и проверочной. Производящую матрицу можно представить двумя подматрицами: информационной и проверочной. Информационная подматрица имеет k столбцов (т. матрица размером kxk), а проверочная – n столбцов. Установлено, что в качестве информационной под матрицы удобно брать единичную матрицу. Количество информационных разрядов k кода Голея равно 12, следовательно, размерность информационной подматрицы Е(х)=2х12. Она имеет вид:
Для построения проверочной подматрицы, которую обозначим как Cr,k, прибегнем к следующему способу: выбираем комбинацию Q(x), содержащую только одну единицу, и делим ее на образующий полином g(x) с получением остатка R(x), который в результате и есть строка проверочной подматрицы.
Допустим, единичный вектор равен 00000000000100000000000, тогда первая строка подматрицы С1(х) получается следующим образом:

C1(x)=R(x)= 01011100011 (3. 11)
Аналогичным образом, сдвигая каждый раз единицу в следующий разряд информационной комбинации, получаем последующие строки проверочной подматрицы С(х).
Данную операцию проводим i=1k раз.
Таким образом, проверочная подматрица имеет вид:
Полученная подматрица С11,12 приписывается справа к единичной подматрице E12, 12 в результате чего получается производящая матрица G23, 12.
Теперь, для кодирования любой комбинации (х) достаточно выбрать из нее разряды, равные 1, и сложить по модулю 2 соответствующие номерам выбранных разрядов строки матрицы G23,12
В циклических кодах, а именно в кодах Голея, процесс кодирования сводится к определению r проверочных разрядов. Каждый проверочный разряд определяется с помощью проверочного соотношения, а определение r проверочных разрядов требует r проверочных соотношений, которые записываются одно под другим в виде проверочной матрицы Нn,r
Проверочная матрица Н может быть построена с помощью проверочного полинома:
где g-1 (x) – полином, сопряженный с образующим полиномом или обратный ему.
h(х)=(х23+1)/(х11+х9+х7+х6+х5+х+1)-1 = х12+х11+х10+х9+х8+х5+х2+1 (3. 13)
что в двоичной форме: 1111100100101.
Последующие строки проверочной матрицы Н получаются с помощью циклического сдвига полученной комбинации, проверочного полинома.
В результате проверочная матрица имеет вид:
Также проверочную матрицу в каноническом виде можно получить из производящей матрицы. Образование этой матрицы производится путем замены строк производящей матрицы на столбцы.
Процесс образования схематично показан стрелками на рис.

рис. 1 Схема образования проверочной матрицы Н
G23,12- производящая матрица
E12,12- информационная подматрица
H23,11 – проверочная матрица
Проверочная матрица обычно используется при построении кодирующих и декодирующих устройств, поскольку она определяет алгоритм нахождения проверочных разрядов по информационным символам.
С помощью проверочной матрицы Н определим проверочные символы при комбинации:
Для вычисления первого проверочного разряда берем первую строку проверочной матрицы:
B1=а2 а5 а8 а9 а10 а11 a12= 1001101=0
B2=а11 а4 а7 а8 а9 а10 а11=1110110=1
B3=а2 а3 а5 а6 а7 а11 а12=1001101=0
B4=а1 а2 а4 а5 а6 а10 а11=1110110=1
B6=а1а3 а5 а7 а8 а9 а12=1001011=0
B7=а4 а5 а6 а7 а9 а10 а12=1011111=0
B8=а3 а4 а5 а6 а8 а9 а11=0101010=1
B9=а2 а3 а4 а5 а7 а8 а10 = 1010101=0
B10=а11 а2 а3 а4 а6 а7 а9 = 1101111=0
B11=а1а3 а6 а9 а10 а11 а12=1011101=1
Таким образом, комбинация линейного кода имеет вид:
Задачей декодера является обратное преобразование принятой поэлементной комбинации циклического кода в исходную k-элементную комбинацию. При этом эффективность циклического кода оценивается его способностью корректировать возникающие при передаче по каналу ошибки.
Декодирование кода Голея можно производить двумя методами:
• декодером Меггита;
• на основе алгоритма Берлекмпа-Месси (в данном случае код Голея рассматривается как разновидность БЧХ).
Декодером Меггита можно однозначно определить и исправить трехкратные ошибки, а алгоритм Берлекемпа-Месси исправляет только двухкратные ошибки. Также необходимо учесть простоту и сравнительную дешевизну аппаратного исполнения декодера Меггита по сравнению с декодером БЧХ. Поэтому в настоящее время в качестве декодера кода Голея используется декодер Меггита.
Принцип работы декодера Меггита основан на «вылавливании» ошибок, расположенных в старших разрядах. При этом должно выполняться следующее условие: длина информационной части не должна превышать длины синдромов ошибок.
Декодер Меггита проверяет синдромы только для тех конфигураций ошибок, которые расположены в старших разрядах. Декодирование ошибок в остальных позициях основано на циклической структуре кода и осуществляется позднее. Соответственно таблица синдромов содержит только те синдромы, которые соответствуют многочленам ошибок с ненулевым коэффициентом en_i. Если вычисленный синдром находится в этой таблице, то en_i исправляется. Затем принятое слово циклически сдвигается и повторяется процесс нахождения возможной ошибки в предшествующей по старшинству позиции (en-i *0). Этот процесс повторяется последовательно для каждой компоненты; каждая компонента проверяется на наличие ошибки, и если ошибка найдена, то она исправляется.
Опишем декодер Меггита для (23,12)-кода Голея.
g(x)=x11+х10+х6+х5+х4+х2+1, получаем S5(x)=x9+x8+x6+x4+x2+x (в двоичной форме 01100110110), S6(x)=x10+x9+x7+x6+x3+x2 (в двоичной форме 00110011011). Следовательно, если ошибка содержится в пятой или шестой позициях, то синдром соответственно равен (01100110110) или (00110011011). Наличие двух дополнительных ошибок в 11 старших разрядах приводит к тому, что в соответствующих позициях два из этих битов заменяются на противоположные.
Декодер отслеживает синдром, отличающийся от нулевого синдрома не более чем в трех позициях, а также синдром, отличающийся от выписанных двух синдромов не более чем в двух позициях.
Допустим, что передавалось кодовое слово
С(х)= 10101010101001100001011.
При передаче часть символов исказилась: V(x)=C(x)+e(x). Многочлен ошибок равен: е(х)=00100000001000000010. Тогда принимаемое слово: V(x)==lo8oi010100001100001o5l, где искаженные символы обозначены значком (*). Определяем синдром S(x)=10011000111.
Рассмотрим второй этап декодирования (где r6(x)=x’6mod g(x)=00110011011, г (х)=х mod g(x)=01100110110). В каждом цикле шаги а,б,в,г -вычисления. На 17 цикле вес Wa=2 и осуществляется исправление ошибок суммированием по модулю 2 содержимого буферного устройства (старшие разряды) с синдромом и 6 символ заменяется на обратный. В это время искаженные два символа находятся в старших разрядах n-разрядах буферного устройства, а третий – в 6 разряде буфера.
Операция вычисления очередного синдрома выполняется следующим образом: анализируется старший разряд синдрома, и если он равен единице, то производится сдвиг содержимого синдрома на 1 разряд влево и суммирование по модулю 2 с образующим полиномом g(x), в противном случае осуществляется только сдвиг синдрома влево.
Принцип построения кода БЧХ
Одним из наилучших среди известных неслучайных кодов, для которых предложены удобные алгоритмы кодирования и декодирования являются коды БЧХ (Боуза-Чоудхури-Хеквингема). Коды БЧХ представляют собой большой класс циклических кодов, исправляющих независимые ошибки кратности t и менее. Для кодов БЧХ характерны все основные свойства циклических кодов.
Свойство 1. Циклический код в полиномиальном его представление можно определить как множество многочленов степени n-1 и меньше, каждый из которых делится без остатка на некоторый многочлен P(x), называемый образующим или порождающим многочленом кода.
Коды БЧХ определяются величинами n, k, d, g(x),
где: n – количество элементов в кодовой комбинации,
k – количество информационных элементов кода БЧХ,
d – количества проверочных разрядов кода БЧХ,
g(x) – порождающий многочлен кода БЧХ.
x15-1 = g1(x) g2(x) g3(x) g4(x)(x-1) (3. 15)
Здесь под неправильным делителем g(x) выписаны их корни, т. среди корней g1(x) и g4(x) содержаться две последовательные степени а, то, что они могут быть выбраны в качестве порождающих многочленов с d0 ≥ = 3. g1(x) и g4(x) имеют соответственно вид:
g1(x)=x4+x2+x+1 (3. 16)
g4(x)=x4+x3+ x2+x+1 (3. 17)
deg g1(x)=4 (т. максимальная степень g1(x)), то длина информационных разрядов равна n-k=4, отсюда k=n-4=15-4=11 получаем код БЧХ (15,11) способный исправить однократную ошибку. Для получения большего n-k=4 необходимо взять в качестве производящего многочлена произведение g2(x) и g4(x), содержащие четыре последовательные степени a: a11, a12, a13, a14.
deg (g2(x), g4(x))=8 отсюда n-k=8 и k=15-8=7. Получаем код БЧХ (15,7) с d0≥5, который может исправлять 2-х кратные ошибки.
Принцип кодирования и декодирования кода БЧХ
Параметры кода БЧХ выбираются следующим образом:
1) Выбирается число n, исходя из формулы n=2m-1, где m – любое целое число.
2) Определяется количество ошибок, которые необходимо исправить
3) В зависимости от величины d0 вычисляется
4) Число проверочных символов вычисляется по формуле: r = m · t.
5) Количество информационных символов k вычисляется по формуле
K = n – r = (2m – 1) – r (3. 19)
Существует несколько способов кодирования кода БЧХ:
1) Любой циклический код задается порождающим многочленом.
Отношение (3. 20) называется проверочным многочленом.
Поскольку g(x) и h(x) однозначно определяют друг друга, код БЧХ может быть задан порождающей и проверочными матрицами.

где Jk – единичная матрица размерности k x k,
Ak2 – матрица коэффициентов уравнений проверок, связывающих значений информационных и проверочных разрядов.
Полученный код является несистематическим, т. код, в котором нельзя разделить информационные разряды от проверочных.
где Bt – значение матрицы проверочных соотношений размерностью k x k
In-1 – единичная матрица размерностью (n – k) x k.
2) Другой способ кодирования кода БЧХ состоит в следующем:
Разделим теперь многочлен Xn-k a(x) на g(x) и запишем делимое в виде
Xn-k a(x) = g(x)q(x) + r(x) (3. 23)
где q(x) – частное,
r(x) – остаток от деления на g(x).
Xn-k a(x) + r(x) = g(x)q(x) (3. 24)
Отсюда получаем искомую кодовую комбинацию разделимого кода БЧХ.
Отличие кодов БЧХ от других циклических кодов состоит в том, что согласно определению коды БЧХ работают с неприводимыми многочленами в поле GF(q), которые могут иметь корни в некотором расширении.
Если q является степенью числа (q = qm), то элементами поля являются все многочлены степени m-1, коэффициенты которых лежат в простом поле GF(р). Поля, которые являются расширением в простом поле GF(q), называются полем Галуа. Элемент поля GF(qm)представляет собой m разрядный вектор с q элементами.
Алгоритм декодирования БЧХ состоит из нескольких этапов:
1) Вычисление синдрома.
2) Вычисление многочлена локатора ошибок.
3) Нахождение корней многочлена локатора ошибок.
4) Исправление ошибок.
Рассмотрим каждый этап.
1) Вычисление синдрома при декодировании можно выполнить двумя способами: с помощью проверочной матрицы Hт или по формуле (3. 25)
Sj = 2n-1 ea2(m+j) (3. 25)
где е – ошибки, а – элементы поля Галуа
Рассмотрим оба способа.
1 С помощью проверочной матрицы Н. Использование проверочной матрицы Hт основано на факте:
где G –каноническая матрица, Hт – транспонированная контрольная матрица. Поэтому если принятое слово принадлежит кодовому множеству, т. в нем отсутствуют ошибки, то

а – элементы поля Галуа.
Для двоичных кодов БЧХ синдромы четных определяются как квадраты предыдущих нечетных синдромов, т. S2 = S12 и т. Если же все синдромы равны S1 – Sq, то ошибок нет.

то, решив её можно определить место расположения ошибок. Данная система уравнений называется ключевыми уравнениями. Известны два наиболее удачных алгоритма вычисления ключевого уравнения Питерсона и Берлекампа – Месси.

Основная черта алгоритма Берлекампа – Месси состоит в следующем: вначале находим самый короткий регистр сдвига L, порождающий с S1 по S0. Далее проверяем, порождает ли этот регистр также S2. Если порождает, то этот регистр по-прежнему остается наилучшим решением, и нужно продолжать проверять, порождает он следующие символы синдрома. На каком-то шаге очередной символ уже не будет порождаться, в этот момент нужно изменить регистр таким образом, чтобы он:
а) правильна, предсказал следующий символ S;
б) не менял предсказаний предыдущих символов;
в) увеличивал длину на максимально возможную величину.
Этот процесс нужно продолжать до тех пор, пока не будутпорождены первые 2t символа синдрома.
Определение локаторов ошибок и, следовательно, корней многочлена локаторов ошибок можно выполнить с помощью процедуры Ченя. Согласно процедуре Ченя, корнем ключевого уравнения должен быть элемент поля Галуа, удовлетворяющий условию (3. 31)
где i-ошибочный символ. Отсюда:
Таким образом, для обнаружения местоположения ошибок необходимо перебрать все элементы поля Галуа GF (2n) и, если n(а-1) = 0, то обратный элемент а1 и будет являться локатором ошибок и укажет место положения ошибки.
Зная место положения, ошибок, производят исправление ошибок согласно формуле:
С^(х) = r(х) + с(х),
где с^ (х) – исправленная кодовая комбинация,
r(х) – принятая кодовая комбинация,
с(х) – вычисленные местоположения ошибок.
Пример реализации кода БЧХ.
В этом примере рассматривается декодирование циклического (7,4,3) кода Хемминга с порождающим многочленом g(x) = х3+х+1. Схема вычисления синдрома показана на Рисунке 3. Принимаемые символы накапливаются в регистре сдвига и одновременно вводятся в схему деления на g(x). После приема седьмого бита содержимое этого регистра сдвигается на один разряд в каждом такте, а схема деления модифицирует синдром и проверяет совпадение с полиномом х6 mod(l+х+х3)= 1+х2 ↔ 101 (в двоичной записи).

Рис. Синдромный декодер двоичного циклического (7,4,3) кода Хэмминга.
Как только на выходе схемы проверки появится 1, будет исправлена ошибка в позиции х6. В тот же самый момент исправление вводится по обратной связи в схему деления и, тем самым, обнуляет остаток от деления. Нулевой остаток может рассматриваться как сигнал об успешном завершении декодирования. Проверка на нулевой остаток схемы деления позволяет обнаруживать некоторые аномалии по окончании процедуры декодирования. Перейдем теперь к изучению циклических кодов, исправляющих многократные ошибки, для которых задача декодирования может рассматриваться как решение системы уравнений. По этой причине здесь необходимо знакомство с полем, в котором будут выполняться операции умножения, сложения и деления. Циклические коды имеют хорошую алгебраическую структуру. Позднее будет показано, что эффективная реализация мощных алгоритмов декодирования достигается при использовании арифметики конечного поля, когда известно размещение корней порождающего многочлена кода.
Напомним, что порождающий полином всегда может быть представлен произведением двоичных неприводимых многочленов:
Алгебраическая структура циклических кодов выражается, в частности, в возможности определения корней каждого из многочленов
в некотором поле разложения (которое является расширением поля, которому принадлежат коэффициенты многочлена). В интересующем нас случае поле разложения неприводимого многочлена является полем Галуа. В литературе поля Галуа называют также конечными полями, имея в виду конечное число принадлежащих ему элементов. Стандартным обозначением является
Определение места ошибки в КК циклического кода
Выбор образующего полинома
При построении циклических кодов важную роль играют образующие полиномы, поскольку они полностью определяют корректирующие свойства кода.
Непроводимыми называются такие полиномы, которые делятся без остатка только на 1 и сами на себя.
Кроме того, среди непроводимых полиномов, отбирают так называемые примитивные.
Примитивные полиномы выбираются из специальных таблиц.
В циклических кодах синдром (остаток) является опознавателем ошибки, но не указывает непосредственно на место ошибки в принятой КК.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется» под полученный остаток таким образом, что в сумме с остатком она дает исправленную комбинацию.
Остаток при этом представляет собой разницу между искаженным и исправленным разрядами. Единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами КК.
Циклически сдвигают искаженную КК до тех пор, пока число единиц в остатке не будет равно числу ошибок, которые может исправлять данный код.
При этом место ошибки не имеет значения. В этом смысле циклические коды могут исправлять пачки ошибок, если длина пачки ошибок не превышает кратность исправляемых ошибок tu
Алгоритм оптимального декодирования на основе анализа веса
Принятая КК делится на образующий полином
Если остаток нулевой, то КК выдается получателю. Если не нулевой, то выполняют п
Производим циклический сдвиг КК влево на один разряд. Делим полученную в результате сдвига КК на образующий полином. Если вес остатка w≤ tu, то складываем остаток с КК и полученную КК сдвигаем вправо на один разряд – будет исправленная КК. Если w> tu, то выполняется п
Повторяем п. 4 до тех пор, пока не будет w≤ tu. КК, полученная в результате последнего циклического сдвига влево, суммируется с последним остатком. Далее выполняется п
Производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута исходная КК относительно принятой КК. В результате получим исправленную КК.
Делим принятую КК на Р(х):
Получим остаток 11, его вес равен 2> tu=1
Производим сдвиг полученной КК влево на 1 разряд
Еще сдвигаем влево КК
Складываем последнее делимое с остатком
Сдвинем эту КК вправо на 4 разряда, т. мы сдвигаем исходную КК влево на 4 разряда:
Получим исправленную КК – сравним с переданной: 1001110
Нахождение ошибок в циклическом коде
нахождение ошибок в коде, наследование#include «stdafx. h» #include «conio. h» #include using namespace std; class.
Изменить порядок в циклическом кодеДобрый день! Написали примитивно программу, нужно исправить, так как при нажатии на кнопку.
Нахождение кратчайшего пути в «циклическом» массивеДобрый вечер! Я пишу простую игру (на Java). Персонаж должен убегать от гангстера. Поле это.
Нахождение ошибокПомогите найти ошибки и переделать код (Сложение чисел) using System. Collections. Generic;.
Вопросы и задачи
Определить кодовое расстояние между комбинациями А иВ и вес каждой комбинации.
Пример. А = 0011011; В = 1000101.
Решение. Вес комбинации равен количеству единиц в слове: ш(А) = 4, ш(В) = 3. Для вычисления кодового расстояния сложим комбинации по модулю 2 и найдем вес суммы. А ® В = 1011110, ш(А ® В) = 6, d = 6.

Алфавит кода состоит из трех разрешенных комбинаций А, В и С. Найти минимальное кодовое расстояние и оценить корректирующую способность кода.
Пример. А = 1011010; 6=1101111; С= 1011001.
Решение. dmin = min <4, 4, 2>= 2. Следовательно, в силу (4. 2), любая однократная ошибка может быть обнаружена. Ошибки более высокой кратности могут не быть обнаружены. Гарантий исправления даже однократных ошибок в этом коде нет, так как не выполняется условие (4. Действительно, ошибки в 6-м или 7-м разрядах комбинаций А и С не исправляется. А вот ошибку в первом или 4-м разрядах можно обнаружить и исправить.

Код Хемминга (7,4) имеет порождающую матрицу:

Пример. Выбрать порождающий полином циклического кода, исправляющего однократные ошибки и позволяющего передать 2000 различных сообщений.
Решение. Определим необходимое количество информационных разрядов из соотношения к > log 2000. к = 11.
По правилу Хемминга (г 2 log (п+ 1), для f = 1) определим, что для исправления однократных ошибок требуется 4 проверочных разряда, следовательно, надо строить (15,11)-код.
Из таблицы примитивных полиномов выбираем порождающий полином д(х) = (х 4 + х + 1), так как он проще других, обеспечивающих ту же корректирующую способность кода.
Пример. Определить количество информационных разрядов кода длиной в пятнадцать символов, если код исправляет две ошибки.
Определите синдром однократной ошибки в 3-м разряде принятой кодовой комбинации.
Помехоустойчивый декодер принял двоичную комбинацию U и вычислил вектор ошибки е. Определите переданное десятичное число.
Блочный код имеет порождающую матрицу G:

Определите синдром двукратной ошибки во втором и шестом разрядах принятого кодового слова.
Помехоустойчивое кодирование. Часть 1

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
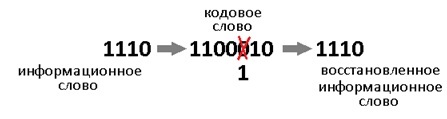
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
Вернер. Основы кодирования (Мир программирования) — 2004 2. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006 3. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Решение
На хабре всё неплохо разжёвано, однако, основные термины считаются сами собой разумеющимися. Типа, «Это происходит вот так, а по какой причине именно так, Вам знать не обязательно».
Код Хэмминга может быть классическим и усечённым.
Количество символов в классическом коде Хэмминга определяется количеством проверочных символов «r». Маркировка какого-либо кода Хэмминга определяется как
Часто некоторое количество символов не используется, такие коды Хэмминга называются усечёнными.
На хабре не объясняется, по какому принципу определяется номер ошибочного символа: собственно, а почему «N через N начиная с N», а не как-то ещё?
Не мудрено, что Вы запутались. Тем не менее, ещё раз перечитайте хабр.
И забудьте о том, до чего Вы там досчитались. Вам по заданию нужно просто выяснить, символ с каким номером в полученном сообщении ошибочный.
Ваш вектор, проверочные символы обозначены красным цветом: 11 0 1 011.
Посимвольно, в виде таблицы:
Имя символаi1 i2 i3i4 i5i6i7 Символ1101011
Вычислим синдромы (проверочные суммы по модулю 2):
S_1=i_1oplus i_3oplus i_5oplus i_7=1oplus 0oplus 0oplus 1=0\\S_2=i_2oplus i_3oplus i_6oplus i_7=1oplus 0oplus 1oplus 1=1\\S_4=i_4oplus i_5oplus i_6oplus i_7=1oplus 0oplus 1oplus 1=1\\ »/>
Синдромы удобнее нумеровать по степеням двойки (то есть, 1, 2, 4, 8, 16 и т. , а не 1, 2, 3, 4 и т. ), поскольку (если ошибка только одна) каждый из синдромов вычисляет один из двоичных разрядов номера ошибочного символа.
В синдром номер 2 попадают символы с номерами 2, 3, 6, 7, в двоичном представлении 0 1 0, 0 1 1, 1 1 0, 1 1 1. Обратите внимание, это все те, у которых 1 во втором разряде (пометил синим).
В синдром номер 4 попадают символы с номерами 4, 5, 6, 7, в двоичном представлении 1 00, 1 01, 1 10, 1 11. Обратите внимание, это все те, у которых 1 в третьем разряде (пометил синим).
Поэтому, если вектор содержит только одну ошибку, то двоичное число, составленное из синдромов, начиная со старшего (в данном случае S4S2S1=110(2)=6(10)), и будет номером ошибочного символа, поскольку распределение символов по суммам синдромов сделано по весам разрядов двоичной системы счисления. Можно (это то же самое, но в «скрытой» форме) сложить номера синдромов, в которых произошло нарушение чётности, и получить номер символа, в котором произошла ошибка: 2+4=6.
Ответ: ошибка в шестом символе, для вычисления верного сообщения нужно инвертировать шестой символ.
