Итак. Задача. Использовать код Хэмминга для двоичного сообщения, длина слова у которого составляет 16 бит. Исходное сообщение возьмём такое «0100010000111101». То есть в слове 16 «букв», каждая из которых может принимать значение либо «0», либо «1».

Двоичный код Хэмминга (Ричард Уэсли Хэмминг –Richard Wesley Hamming), систематический код, имеет кодовое расстояние d = 3 и позволяет обнаруживать и исправлять одиночную ошибку.
Корректирующие коды обозначают (n,k), где n – количество символов в кодовой комбинации, из них k – количество информационных символов.
Коды Хэмминга для r проверочных символов
т.е. (7, 4), (15, 11), (31,26) и т.д.
Построение кодов Хэмминга основано на принципе проверки на четность числа единичных символов: каждый проверочный символ представляет собой сумму по модулю 2 некоторой подпоследовательности информационных символов.

Тогда для преобразования
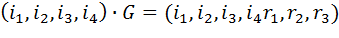
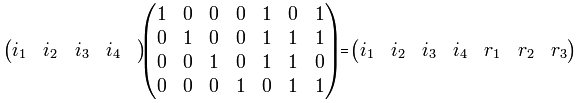
В декодере строится вектор-синдром (S1, S2, S3)

Если синдром равен «0» т.е. (0, 0, 0), то это означает, что ошибки нет.
Если синдром отличен от нуля, то по таблице синдромов можно найти позицию ошибки:

Рассмотрим еще один вариант, который иногда только и называется кодом Хэмминга (т.е. предыдущий вариант в этом смысле – не код Хэмминга).
Код сначала зададим при помощи его проверочной матрицы.
Рассмотрим матрицу Н из нулей и единиц, содержащую m = 3 строки и 2m — 1= 7 столбцов, причем столбцами являются все ненулевые двоичные наборы длины т, записанные так, что номер столбца записан в двоичной системе счисления в этом столбце
Число проверочных символов составляет r = 3, число информационных символов равно 4, а общее количество бит в кодовой комбинации = 7.
Код по определению является разделимым (систематическим), т.е. в нем явным образом заданы информационные и проверочные символы.
Можно было бы задать например I1I2I3I4P1P2P3, но так делать нецелесообразно.
Кодирование легко проводится, если в качестве проверочных выбраны первый, второй и четвертый символы, так как в этом случае каждый из этих символов входит только в одно из проверочных соотношений, задаваемых матрицей Н. Т.е. используют следующую последовательность: P1P2I1P3I2I3I4.
Чтобы рассчитать P1P2 и P3, следует решить следующую систему уравнений, которая при данной последовательности распадается на отдельные уравнения.
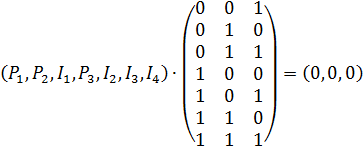
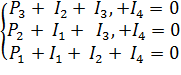

Если при принятой нами проверочной матрице H взять последовательность I1I2I3I4P1P2P3 , то система не распадется на три независимых уравнения.
Полученные уравнения для P1P2P3 позволяют воссоздать порождающую код матрицу G
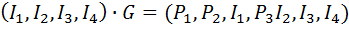

Рассмотрим обнаружение ошибок.
Предположим, что передавался кодовый вектор u и появилась одна ошибка. Тогда будет получен вектор u + е, где е — вектор, содержащий «1» в том разряде, где произошла ошибка, и «0» во всех остальных разрядах.
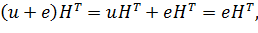
так как u — кодовый вектор и поэтому принадлежит нулевому пространству матрицы Н и
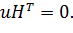
Но поскольку е — вектор, содержащий единственную единицу в разряде, соответствующем ошибке, то синдром еНТ равен как раз той строке матрицы НТ,которая соответствует ошибке.
Таким образом, сравнивая синдром с матрицей НТ,можно найти положение ошибки и затем исправить ее, просто заменив соответствующий символ на правильный.
Особенно удобно это делать, если использовать в качестве i-гo столбца матрицы Н двоичное представление числа i. Тогда для каждой отдельной одиночной ошибки синдром является двоичным представлением номера разряда, в котором произошла ошибка. Это расположение первоначально использовано Хэммингом.
Пример. Чтобы закодировать информационные символы 1100, нужно определить проверочные символы в слове P1 P2 1 Р3 1 0 0. Кодовый вектор равен 0111100.
Предположим, что пятый символ принят ошибочно, тогда будет получен вектор 0111000. Легко вычислить синдром, который оказывается равным 101 — величине, соответствующей пятому столбцу матрицы Н и указывающей на то, что ошибка произошла в пятом символе полученного вектора. Синдром является двоичным кодом числа 5, поскольку каждый столбец матрицы Н выбирался как двоичное представление номера столбца.

– Нарисовать структурную схему кодера и декодера, исправляющего ошибку.
– Исправить ошибку, допущенную в четвертом элементе принятой кодовой комбинации.
Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока. Поясним идею проверки на чётность на примере простейшего корректи-рующего кода, который так и называется кодом с проверкой на чётность иликодом с проверкой по паритету (равенству).В таком коде к кодовым комбинациям безизбыточного первичного двоич-ного k – разрядного кода добавляется один дополнительный разряд (символпроверки на чётность, называемый проверочным, или контрольным). Если чис-ло символов “1” исходной кодовой комбинации чётное, то в дополнительномразряде формируют контрольный символ 0, а если число символов “1” нечёт-ное, то в дополнительном разряде формируют символ 1. В результате общеечисло символов “1” в любой передаваемой кодовой комбинации всегда будет чётным.Таким образом, правило формирования проверочного символа сводится кследующему:
где i – соответствующий информационный символ (0 или 1), k – общее их числоа под операцией “⊕” здесь и далее понимается сложение по mod2. Очевидно,что добавление дополнительного разряда увеличивает общее число возмож-ных комбинаций вдвое по сравнению с числом комбинаций исходного первич-ного кода, а условие чётности разделяет все комбинации на разрешённые инеразрешённые. Код с проверкой на чётность позволяет обнаруживать одиноч-ную ошибку при приёме кодовой комбинации, так как такая ошибка нарушаетусловие чётности, переводя разрешённую комбинацию в запрещённую.Критерием правильности принятой комбинации является равенство нулюрезультата S суммирования по mod 2 всех n символов кода, включая провероч-ный символ r1. При наличии одиночной ошибки S принимает значение 1:
S = r1 ⊕ i1 ⊕ i2 ⊕ . . . ⊕ ik = 0 – ошибки нет
1444424443 = 1 – однократная ошибка. n
r1 = i1 ⊕ i2 ⊕ i3;
r2 = i2 ⊕ i3 ⊕ i4;
r3 = i1 ⊕ i2 ⊕ i4,
В соответствии с этим алгоритмом определения значений проверочныхсимволов ri ниже выписаны все возможные 16 кодовых слов (7,4) – кода Хем-минга.
На рис. 3.3 приведена схема декодера для (7,4) – кода Хемминга, на входкоторого поступает кодовое слово
V = ( i1′, i2′, i3′, i4′, r1′, r2′, r3′)
Апостроф означает, что любой символ слова может быть искажён помехой вканале передачи.
В декодере в режиме исправления ошибок строится последовательность:
s1 = r1′ ⊕ i1′ ⊕ i2′ ⊕ i3′;
s2 = r2′ ⊕ i2′ ⊕ i3′ ⊕ i4′;
s3 = r3′ ⊕ i1′ ⊕ i2′ ⊕ i4′. Трёхсимвольная последовательность ( s1, s2, s3 ) называется синдромом.
Термин “синдром” используется и в медицине, где он обозначает сочетаниепризнаков, характерных для определённого заболевания. В данном случаесиндром S = (s1, s2, s3 ) представляет собой сочетание результатов проверкина чётность соответствующих символов кодовой группы и характеризует опре-делённую конфигурацию ошибок (шумовой вектор).
Кодовые слова (7,4) – кода Хемминга.
к = 4 r = 3
i1 i2 i3 i4 r1 r2 r3
0 0 0 0 0 0 0
0 0 0 1 0 1 1
0 0 1 0 1 1 0
0 0 1 1 1 0 1
0 1 0 0 1 1 1
0 1 0 1 1 0 0
0 1 1 0 0 0 1
0 1 1 1 0 1 0
1 0 0 0 1 0 1
1 0 0 1 1 1 0
1 0 1 0 0 1 1
1 0 1 1 0 0 0
1 1 0 0 0 1 0
1 1 0 1 0 0 1
1 1 1 0 1 0 0
1 1 1 0 1 1 1
Число возможных синдромов определяется выражением S = 2r. (3.21)
При числе проверочных символов r = 3 имеется восемь возможных син-дромов (23 = 8). Нулевой синдром (000) указывает на то, что ошибки при приёмеотсутствуют или не обнаружены. Всякому ненулевому синдрому соответствуетопределённая конфигурация ошибок, которая и исправляется. Классическиекоды Хемминга (3.20) имеют число синдромов, точно равное их необходимомучислу, позволяют исправить все однократные ошибки в любом информативноми проверочном символах и включают один нулевой синдром. Такие коды назы-ваются плотноупакованными.Усечённые коды являются неплотноупакованными, так как число синдро-мов у них превышает необходимое. Так, в коде (9,5) при четырёх проверочныхсимволах число синдромов будет равно 24 =16, в то время как необходимо все-го 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5).
Для рассматриваемого кода (7,4) в таблице 1 представлены ненулевыесиндромы и соответствующие конфигурации ошибок.
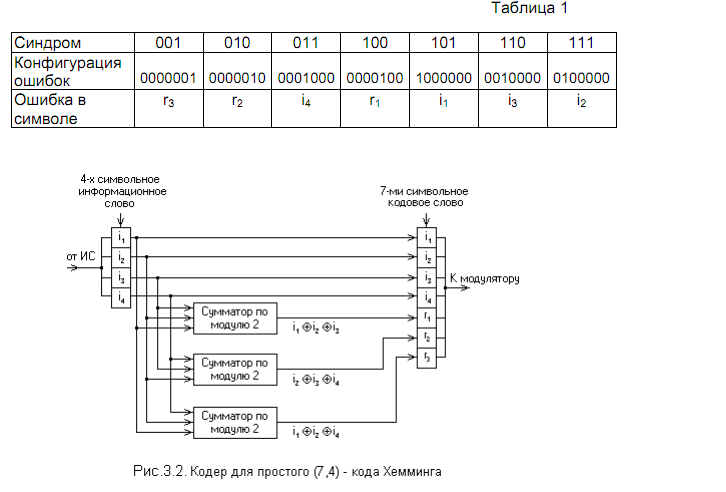
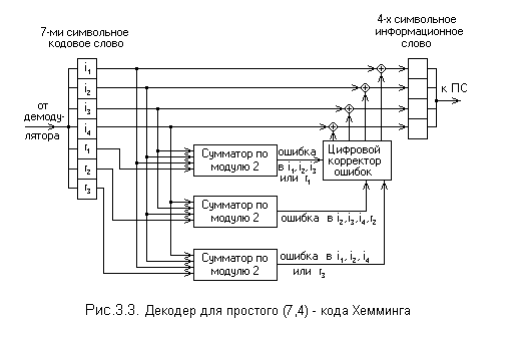
Таким образом, код (7,4) позволяет исправить все одиночные ошибки.Простая проверка показывает, что каждая из ошибок имеет свой единственныйсиндром. При этом возможно создание такого цифрового корректора ошибок(дешифратора синдрома), который по соответствующему синдрому исправляетсоответствующий символ в принятой кодовой группе. После внесения исправ-ления проверочные символы ri можно на выход декодера (рис.3.3) не выводить.Две или более ошибки превышают возможности корректирующего кода Хем-минга, и декодер будет ошибаться. Это означает, что он будет вносить не-правильные исправления и выдавать искажённые информационные символы.Идея построения подобного корректирующего кода, естественно, не меня-ется при перестановке позиций символов в кодовых словах. Все такие вариан-ты также называются (7,4) – кодами Хемминга
Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H(n,k), имеющей
столбцов, причем столбцами H(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до
Длина кодовой комбинации кода Хэмминга равна
Число информационных элементов определяется как
Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.
Зная вид матрицы H(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбца H(n,k) не являются линейно зависимыми. Наряду с этим, для любого числа m всегда можно указать три столбца матрицы H(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэмминга dmin=3.
Код Хэмминга является одним из немногочисленных примеров совершенного кода.
Действительно, поскольку (n, k) – код Хэмминга исправляет все одиночные ошибки, то все образцы одиночных ошибок (а их всего насчитывается
вариантов) должны разместиться в различных смежных классах, число которых также равно
При фиксированном числе
можно построить код Хэмминга любой длины (
) путем укорочения (n, k) – кода. Укорочение не уменьшает минимальное кодовое расстояние. В силу того, что для любого числа n существует код Хэмминга, любой групповой код с исправлением одиночных ошибок принято называть кодом Хэмминга.
Пример 5.13. Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.
Очевидно, что минимальная длина кода Хэмминга, имеющего практическое значение, есть 3. При увеличении n отношение
Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:
Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3( к примеру 1, 2 и 3), следовательно, dmin=3.
В том случае, когда столбцы матрицы H(n,k) – кода Хэмминга есть упорядоченная запись m – разрядных двоичных чисел, декодирование осуществляется оригинальным образом. В результате вычисления проверочного соотношения для кодовой комбинации
, имеющей одиночную ошибку, получается синдром
в точности равный номеру элемента, в котором произошла ошибка.
Действительно, если ei содержит одну единицу в разряде, соответствующем ошибочному элементу, то при умножении на матрицу НТ все строки матрицы НТ, соответствующие нулям в ei, обращаются в нули, и лишь строка, соответствующая “1” в ei сохраняет свой вид (т.е. порядковый номер элемента в двоичной записи) в ответе.
Пример 5.15. Пусть приемник УЗО системы передачи данных зарегистрировал комбинацию
т.е. ошибка в четвертом элементе и кодовая комбинация кода (7,4), которая была передана, имеет вид:
Путем несложных преобразований из (n, k) – кода Хэмминга с dmin=3 можно получить (n+1, k) – код Хэмминга с dmin=4.
Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.
Матрица проверок для (n+1, k) – кода Хэмминга с dmin=4 получается из матрицы проверок (n, k) – кода с dmin=3 путем введения дополнительной строки из (n+1)-ой единицы.
Так как размерность матрицы проверок кода с dmin=4 должна быть равна
, то к каждой строке матрицы проверок кода с dmin=3, необходимо добавить один нулевой элемент для того, чтобы не нарушить введенные ранее проверки. Матрица проверок для (n+1, k) – кода dmin=4 имеет вид:
Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.
Пример 5.16. Построить код Хэмминга (8,4) с dmin=4 на основе матрицы проверок кода (7,4).
По виду матрицы
можно сделать вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на четность.
Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.
Таким образом, матрице
Для того, чтобы получить код (8,4) с dmin=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:
Определим известным способом dmin (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) dmin=4.
До сих пор мы еще не разделили элементы кодовой комбинации на информационные и проверочные. Наиболее рационально, по-видимому, это можно сделать следующим образом. Желательно, чтобы каждое проверочное соотношение однозначно определяло проверочный элемент как результат проверки на четность некоторой совокупности информационных элементов. В таком случае мы получили бы возможность определять значение проверочного элемента наиболее простым образом – решением одного линейного уравнения с одним неизвестным. Для этого при упорядоченной записи столбцов матрицы H(n,k) в качестве проверочных элементов необходимо брать элементы с номерами 2i, где i изменяется от 0 до m-1, так как именно эти столбцы содержат только по одной единице. Последнее свидетельствует о том, что элементы с номерами 2i входят только в одну проверку и, следовательно, они могут быть взяты в качестве проверочных.
Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).
Зная места проверочных элементов, легко привести матрицу H(n,k) кода Хэмминга к канонической форме.
Для этого необходимо столбцы с номерами 2i, где
Пример 5.18. Преобразовать матрицу
Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:
Это и есть каноническая форма матрицы
. Сравнение ее с исходной матрицей
показывает, что местам информационных элементов в канонической форме соответствуют столбцы с номерами 3, 5, 6, 7, а местам проверочных элементов – столбцы 4, 2, 1.
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:
Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.
Оценим эффективность кодов Хэмминга.
Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратности S=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:
Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:
Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:
Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:
На основе (n, n-1) – кодов с dmin=2 или кодов Хэмминга с dmin=3 и dmin=4 можно построить коды с более высокими корректирующими свойствами. Для этой цели, наряду с защитой каждой передаваемой комбинации описанным выше способом, осуществляют помехоустойчивое кодирование одноименных разрядов групп передаваемых комбинаций. Процесс кодирования можно пояснить при помощи рис. 5.6.
Комбинации простого кода, подлежащие передаче по системе связи, записываются в виде таблицы – каждая комбинация составляет отдельную строку этой таблицы (информационные символы). Затем осуществляется кодирование по строкам и столбцам. В общем случае для кодирования строк и кодирования столбцов можно использовать различные коды. Избыточные элементы дописываются к каждой строке (проверка по строкам) и к каждому столбцу (проверка по столбцам). Проверка проверок осуществляется кодированием столбцов, составленных из избыточных элементов строк или кодированием строк, составленных из проверок столбцов. Последующее введение избыточности осуществляется для защиты блоков информации, представленных на рис. 5.6. Процесс кодирования поясняется на рис. 5.7. Из блоков информации, защищенных двумя проверками, составляется параллелепипед. Избыточные разряды третьей проверки образуют параллелепипед, выделенный утолщенной линией.
5 эл. комбинация
В результате итеративного кодирования получаются групповые коды, которые обладают следующим важным свойством.
Теорема 5.3. Минимальное кодовое расстояние итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.
Действительно, если в случае двух проверок минимальный вес одного кода равен
, а другого
, то вектор итеративного кода имеет, по крайней мере,
единиц в каждой строке и
элементов в каждом столбце и, следовательно, не менее
Аналогичные рассуждения можно продолжить и на случай большего числа проверок.
Порождающая матрица итеративного кода может быть построена следующим образом.
Пусть GA – порождающая матрица кода, используемого для проверки по строкам, а GВ – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (GAВ) имеет вид:
означает, что на местах “1” в матрице GA записывается матрица GВ, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам GВ. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то
Декодирование
А теперь представим, что к нам пришло сообщение с ошибкой. Вот оно «100110001100001011101».
Мы знаем, что в него добавлены избыточные биты по алгоритму Хемминга, и нам надо проверить, есть в нём ошибка или нет.
Для этого нужно поступить следующим образом. Сначала вычисляем заново все контрольные биты по предыдущему алгоритму.
Для этого сначала обнуляем все биты, находящиеся на номерах степеней двойки:

В первом оставляем нуль, ибо в подконтрольных битах чётное число единиц.

Вычисляем все остальные контрольные биты по описанному выше алгоритму (мне лень заново его описывать тут), и получаем, что не совпадают контрольные биты под номерами 1 и 8:

Теперь складываем номера этих контрольных бит: 1 + 8, и получаем 9 — номер бита, в котором закралась ошибка! Ура! Теперь просто меняем девятый бит на обратный — с единицы на нуль, — и получаем исходное сообщение!
Отметим, что это самый простейший алгоритм Хемминга, который может исправить только одну ошибку в слове. Об остальных алгоритмах данная статья умалчивает. 🙂
Сначала в исходное сообщение добавляем контрольные биты и устанавливаем их в нуль.
Контрольные биты располагаются в тех номерах битов, которые равны степеням двойки (ибо алфавит двоичный).
То есть. Два в степени нуль — это единица, два в степени 1 = два, два в степени 2 = четыре, а два в степени 3 = восемь, два в степени 4 = 16
Значит контрольные биты будут находиться в «буквах»(битах) под номерами 1, 2, 4, 8 и 16.

В остальные номера бит переписываем исходное сообщение.

Видно, что длина «слова» из-за такой избыточности увеличилась на пять «букв». В данном случае, конечно. У вас количество дополнительных бит будет зависеть от длины исходного «слова».
Теперь нужно вычислить эти контрольные биты.
Каждый контрольный бит с номером N «контролирует» непрерывную последовательность из N битов, через каждые N битов.
Вот на картинке отмечено иксами (X), какие биты нужно использовать для вычисления первого контрольного бита (с номером «1»)

Для вычисления контрольно бита нужно просто сложить все «буквы» нашего «слова», которые он контролирует, а затем принять нелёгкое решение: если сумма получилась чётная, то пишем в результате нуль, а если нечётная — единицу.
Вычисляем первый бит.
Складываем биты под номерами 3,5,7,9,11,13,15,17,19,21
Это будет 0 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 = 5
Получилось 5 (пять). Сумма нечётная (на два нацело не делится). Значит пишем в первый бит единицу:

Теперь вычислим контрольный бит номер 2. Для него нужно будет найти сумму каждых двух бит следующих друг за другом непрерывно, через каждые два бита. Такие биты я тоже отметил на картинке.

То есть будем теперь суммировать биты, начитая с третьего по номеру, и далее те, которые отмечены иксом (X).
Их номера 3, 6, 7, 10, 11, 14, 15, 18, 19.
Это будет 0 + 0 + 0 + 1 + 0 + 0 + 1 + 1 + 1 = 4
Четыре — число чётное, значит оставляем в нашем втором бите нуль.

Переходим к вычислению третьего контрольного бита. Но это у нас он контрольный — третий. А в сообщении этот бит записан под номером 4 — четыре.

Значит и использовать будем все попадающие под наше правило биты, начиная с пятого.
А это биты под номерами 5, 6, 7, 12, 13, 14, 15, 20, 21.
Складываем их: 1 + 0 + 0 + 0 + 0 + 0 + 1 + 0 + 1 = 3
В итоге у нас нечётное число, значит пишем в наш контрольный бит единицу.

Осталось всего ничего — вычислить два оставшихся контрольных бита, которые под номерами 8 и 16.
В восьмом оставляем нуль потому, что в той последовательности, которую мы используем для вычисления присутствуют две единицы, дающие в сумме чётное число.

А в 16-м тоже сумма бит получается чётной — оставляем нуль:

В итоге мы получили слово с кодом Хэмминга, которое содержит избыточные биты (в сумме 21): «100110000100001011101».
