Выбор образующего полинома
При построении циклических кодов важную роль играют образующие полиномы, поскольку они полностью определяют корректирующие свойства кода.
Как мы уже отмечали остаток от деления КК циклического кода на образующий полином является синдромом этого кода. Для того, чтобы код мог исправлять ошибки, количество ненулевых остатков должно быть равно количеству комбинаций с различным сочетанием ошибок. Если код исправляет однократную ошибку, то число различных остатков равно количеству элементов в КК длиной «n». В общем случае число различных остатков должно быть равно Сntи. Поэтому в качестве образующих полиномов берутся многочлены из класса непроводимых.
Непроводимыми называются такие полиномы, которые делятся без остатка только на 1 и сами на себя.
Кроме того, среди непроводимых полиномов, отбирают так называемые примитивные.
Примитивным считается полином степени r, если он обеспечивает максимальное число непроводимых полиномов той же степени r. Таких остатков должно быть не менее 2r-1/
Примитивные полиномы выбираются из специальных таблиц.
МККТТ рекомендует V.41 – P(x)= x16+x12+ x5+1 – «Аккорд 1200»
В циклических кодах синдром (остаток) является опознавателем ошибки, но не указывает непосредственно на место ошибки в принятой КК.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется» под полученный остаток таким образом, что в сумме с остатком она дает исправленную комбинацию.
Остаток при этом представляет собой разницу между искаженным и исправленным разрядами. Единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами КК.
Циклически сдвигают искаженную КК до тех пор, пока число единиц в остатке не будет равно числу ошибок, которые может исправлять данный код.
При этом место ошибки не имеет значения. В этом смысле циклические коды могут исправлять пачки ошибок, если длина пачки ошибок не превышает кратность исправляемых ошибок tu
Алгоритм оптимального декодирования на основе анализа веса
1. Принятая КК делится на образующий полином
2. Если остаток нулевой, то КК выдается получателю. Если не нулевой, то выполняют п.3
5. Повторяем п.4 до тех пор, пока не будет w≤ tu. КК, полученная в результате последнего циклического сдвига влево, суммируется с последним остатком. Далее выполняется п.6
6. Производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута исходная КК относительно принятой КК. В результате получим исправленную КК.
1. Делим принятую КК на Р(х):
2. Производим сдвиг полученной КК влево на 1 разряд
делим на Р(х)
3. Еще сдвигаем влево КК
4. Еще сдвигаем влево КК
5. Еще сдвигаем влево КК
1 – вес остатка w= tu =1
6. Складываем последнее делимое с остатком
7. Сдвинем эту КК вправо на 4 разряда, т.к. мы сдвигаем исходную КК влево на 4 разряда:
Получим исправленную КК – сравним с переданной: 1001110
Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов:
если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.
Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.
Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Представление кодовой комбинации в виде многочлена.
Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов).
В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде
Запишем полиномы для конкретных 4-элементных комбинаций
Действия над многочленами.
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,
Рассмотрим операцию деления на следующем примере:
Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.
Отметим, что запись кодовой комбинации в виде многочлена, не всегда определяет длину кодовой комбинации. Например, при n = 5, многочлену
Алгоритм получения разрешенной кодовой комбинации циклического кода из комбинации простого кода
Пусть задан полином
, определяющий корректирующую способность кода и число проверочных разрядов r, а также исходная комбинация простого k-элементного кода в виде многочлена
Требуется определить разрешенную кодовую комбинацию циклического кода (n, k).
1. Умножаем многочлен исходной кодовой комбинации на
2. Определяем проверочные разряды, дополняющие исходную информационную комбинацию до разрешенной, как остаток от деления полученного в предыдущем пункте произведения на образующий полином
3. Окончательно разрешенная кодовая комбинация циклического кода определится так
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация – разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки, ее местоположении и исправить ошибку.
Формирование базиса (производящей матрицы) циклического кода
Формирование базиса циклического кода возможно как минимум двумя путями.
1. Составить единичную матрицу для простого исходного кода.
2. Определить для каждой кодовой комбинации исходного кода группу проверочных элементов и дописать их в соответствующие строки матрицы.
Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).
1. Дописать слева от КК, соответствующей образующему полиному циклического кода нули так, чтобы длина разрешенной кодовой комбинации равнялась n.
2. Получить остальные разрешенные кодовые КК базиса, используя циклический сдвиг исходной. (В базисе должно быть k – строк)
В данном случае код будет неразделимым.
Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом
Построение кодера циклического кода
Рассмотрим код (9,5) образованный полиномом
Разрешенная комбинация циклического кода
образуется из комбинации простого (исходного) кода путем умножения ее на
и прибавления остатка R(x) от деления
1. Умножение полинома на одночлен
эквивалентно добавлению к двоичной последовательности соответствующей G(x) , r – нулей справа.
Для реализации операции добавления нулей используется r-разрядный регистр задержки.
2. Рассмотрим более подробно операцию деления:
Это двоичное число и будет остатком
Построение формирователя остатка циклического кода
Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.
Сформулируем правила построения ФПГ.
1. Число ячеек памяти равно степени образующего полинома r.
2. Число сумматоров на единицу меньше веса кодирующей комбинации образующего полинома.
3. Место установки сумматоров определяется видом образующего полинома.
Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.
4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.
Структурная схема кодера циклического кода (9,5)
Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.
Рассмотрим работу этой схемы
1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4
2. Во время пятого такта К2 – замыкается а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.
За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток
3. К2 – размыкается, К1 – замыкается и в след за информационными в линию уйдут элементы проверочной группы.
4. Одновременно идет заполнение регистров новой комбинацией.
Второй вариант построения кодера ЦК.
Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.
Устройство деления на производящий полином
За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).
За эти же 5 тактов информационные разряды, выданные сразу на модулятор.
Далее в след за информационными уходят проверочные из ячеек устройств деления.
Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.
Окончательно структурная схема экономичного кодера выглядит так.
– На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.
– После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;
– на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.
Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.
Определение ошибочного разряда в ЦК.
Пусть А(х)-многочлен соответствующий переданной кодовой комбинации.
Н(х)- многочлен соответствующей принятой кодовой комбинацией.
Тогда сложение данных многочленов по модулю два даст многочлен ошибки.
При однократной ошибке Е(х) будет содержать только один единственный член соответствующий ошибочному разряду.
Остаток – полученный от деления принятого многочлена H(x) на производящей Pr(x) равен остатку полученному при делении соответствующего многочлена ошибок E(x) на Pr(x)
При этом ошибке в каждом разряде будет соответствовать свой остаток R(x) (он же синдром), а значит, получив синдром можно однозначно определить место ошибочного разряда.
Алгоритм определения ошибки.
Пусть имеем n-элементные комбинации (n = k + r) тогда:
2. Делим полученный полином Н(х) на Pr(x) и получаем текущий остаток R(x).
3. Сравниваем R0(x) и R(x).
– Если они равны, то ошибка произошла в старшем разряде.
– Если “нет”, то увеличиваем степень принятого полинома на Х и снова проводим деления
в) Опять сравниваем полученный остаток с R0(x)
– Если они равны, то ошибки во втором разряде.
– Если нет, то умножаем Н(х)х2 и повторяем эти операции до тех пор, пока R(X) не будет равен R0(x).
Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.
то номер ошибочного разряда 3+1=4
Пример декодирования комбинации ЦК.
Положим, получена комбинация H(х)=111011010
Проанализируем её в соответствии с вышеприведенным алгоритмом.
Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х8 на производящий полином P(x)=X4+X+1
Разделим принятую комбинацию на образующий полином
Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.
Декодер циклического кода с исправлением ошибки
Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ.
Если во втором по старшинству то после 10го; в третьем по старшинству то после 11го; в четвертом по старшинству то после 12го в пятом по старшинству то после 13го в шестом по старшинству то после 14го в седьмом по старшинству то после 15го в восьмом по старшинству то после 16го в девятом по старшинству то после 17го.
На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.
Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.
В нашем случае инвертируется второй разряд на 11 такте.
1.Используя матричное представление построить контрольную матрицу для линейного кода (11,7).
Решение: линейные коды обозначают как
– значность кодовой комбинации, а
– число информационных символов в ней. Согласно заданию имеем:
Строим порождающую матрицу:
2.Построить контрольную матрицу линейного кода, ориентированного на исправление однократных ошибок. Требуемый объем кода Q=40.
Определяем требуемое число информационных разрядов:
Так как код должен исправлять только одиночные ошибки, определение числа контрольных разрядов осуществляется в соответствии с выражением:
3.Из канала связи поступила комбинация линейного кода
Находим синдром ошибки
Итак, синдром ошибки
. Он совпадает с 1-м столбцом контрольной матрицы, следовательно, ошибка произошла в этом разряде. Исправляем этот разряд
. По контрольной матрице определяем, что контрольными разрядами являются 2, 3 и 7 разряды. Следовательно, информационная часть имеет вид 0111=
. Передавалось число
4.Закодировать линейным кодом число
В формируемой комбинации контрольными разрядами будут
(соответствуют столбцам контрольной матрицы с одной 1). Составляем выражение для определения контрольных разрядов. Для того, чтобы формируемый кодовый вектор был ортогонален вектору
будет достигнута, если
В окончательном виде
5.Закодировать циклическим кодом
, образующий многочлен
Разрешенные комбинации циклического кода формируются в соответствии с выражением:
– остаток от деления многочлена
В виде кодовых векторов указанные многочлены имеют вид:
в виде КВ имеет вид:
Из канала связи поступила комбинация ЦК 1001100,
Находим остаток от деления принятого КВ на
имеет 3 ненулевых члена, следовательно, кодовое расстояние кода, порождаемое этим многочленом,
и код способен исправлять только однократные ошибки, т.е.
Имеем: вес остатка
. Следовательно, принятую комбинацию нужно смещать циклически влево и вновь делить на
Требуется еще сдвиг:
и сдвигаем в обратную сторону на 3 такта:
. Контрольные разряды отбрасываем. Получаем:
7.Построить схему делителя на образующий многочлен
Циклический код относится к классу
систематических кодов. Ранее было
показано, что при обнаружении одиночной
ошибки минимальное кодовое расстояние
равно
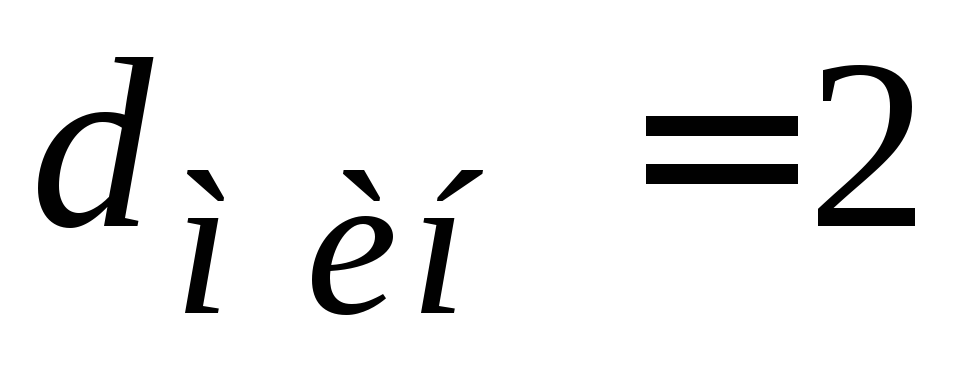
Код однократной ошибки
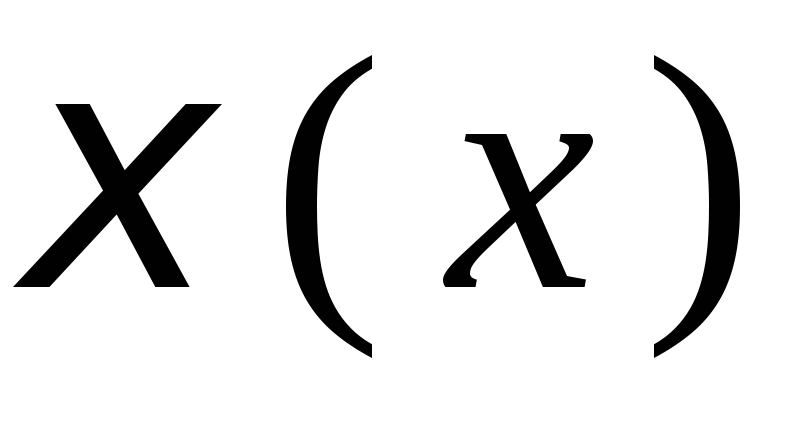
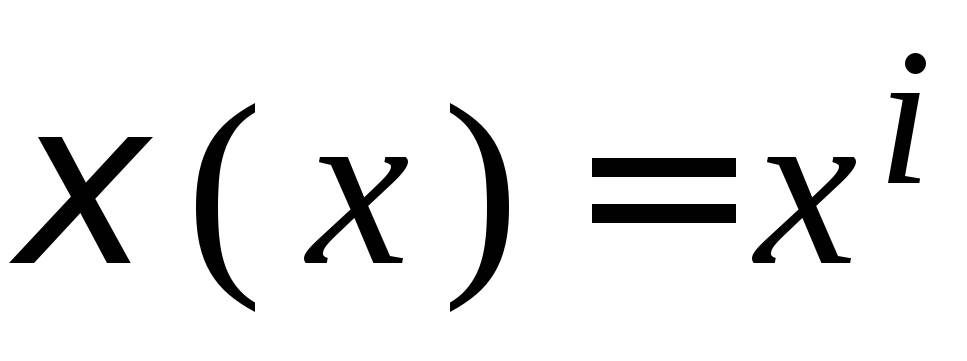
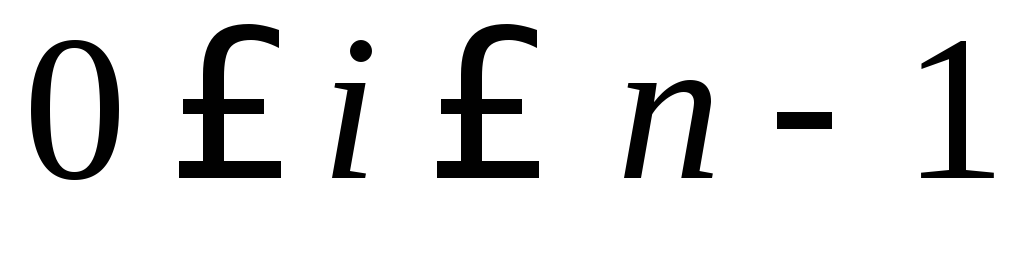
.
Код ошибки суммируется по модулю два с
одним из символовn-разрядной
кодовой комбинации
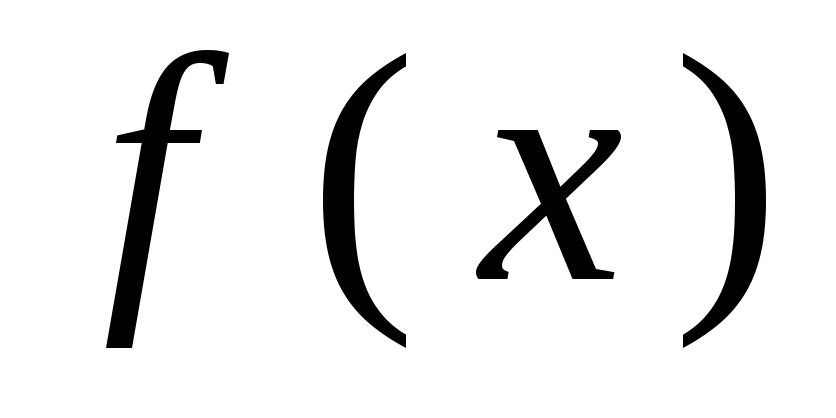
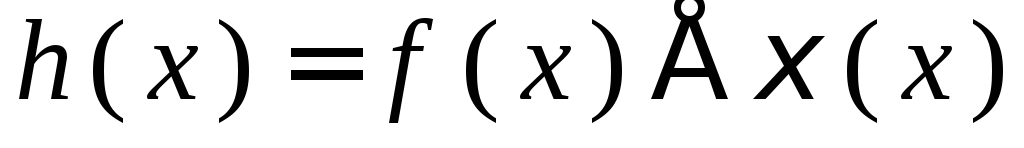
Среди всех неприводимых полиномов
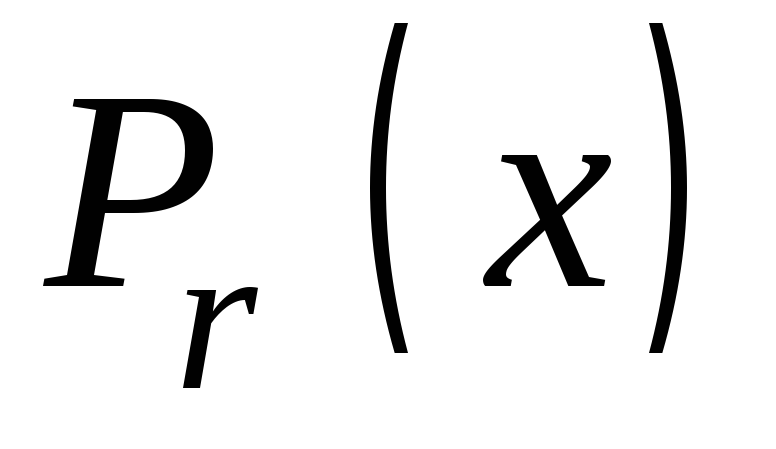
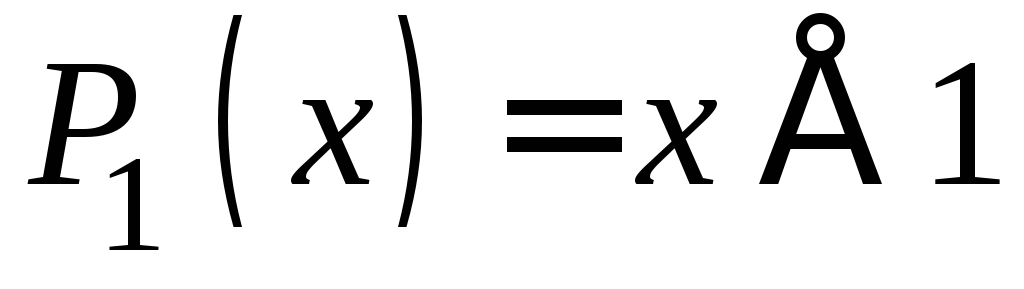
обладает наименьшей степенью. Двоичный
код, соответствующий этому полиному,
записывается как 11. При делении любого
полинома степени
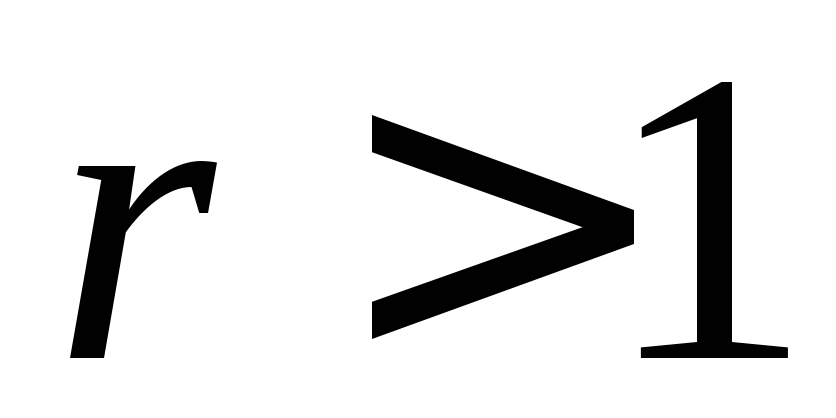
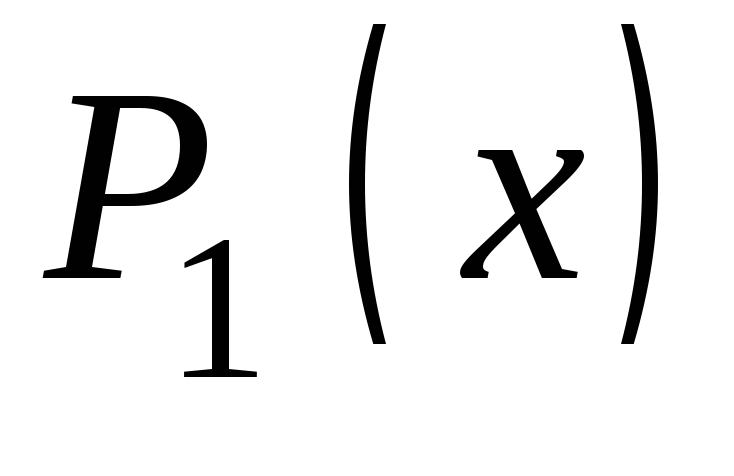
Образование кода. Положим
– код, проверочный символ которого
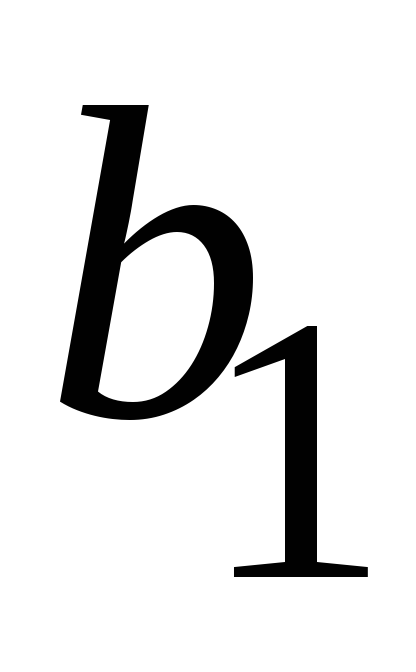
неизвестен. Разделим кодовую комбинацию
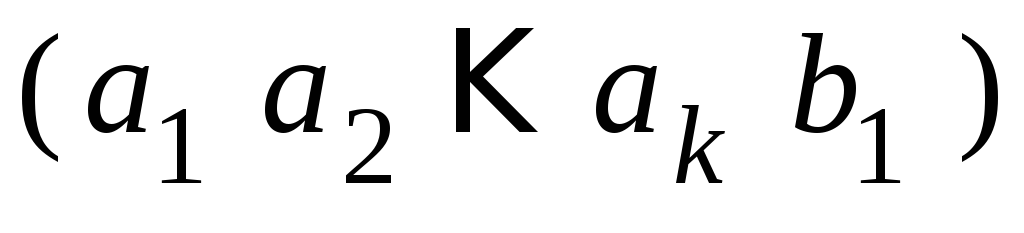
на код 11 неприводимого полинома
.
В результате деления получится остаток.
Проверочный символ
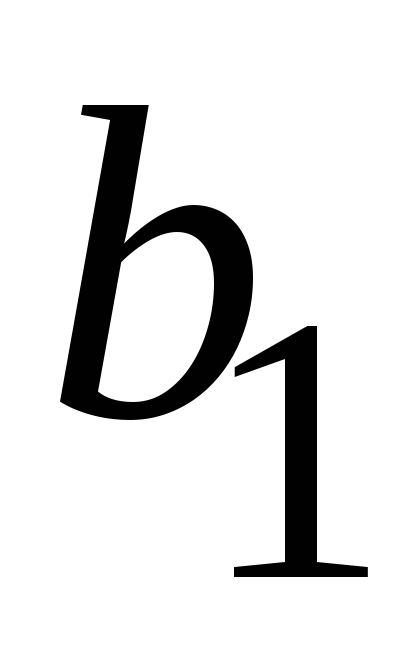
Например, пусть кодовая комбинация
101 представляет информационные символы.
На рисунке 5.6 представлена процедура
определения значения символа
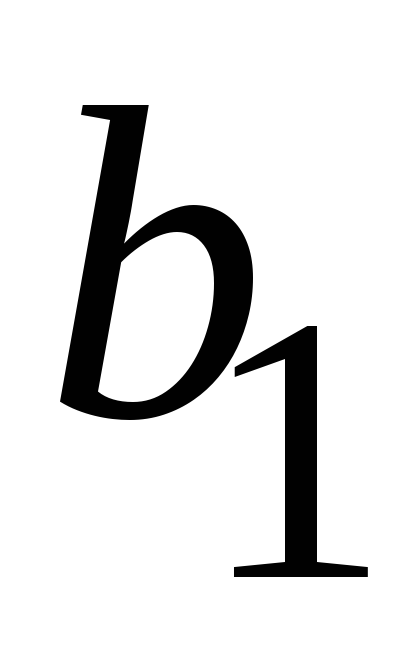
.
Последняя строка на этом рисунке –
остаток, равный нулю, поэтому символ
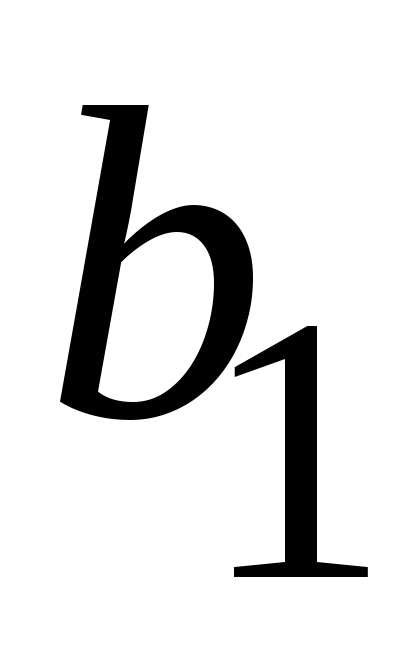
На рисунке 5.7 представлена процедура
обнаружения однократной ошибки. Ошибка
в коде обозначена жирным шрифтом. В
результате деления кода с ошибкой на
неприводимый полином
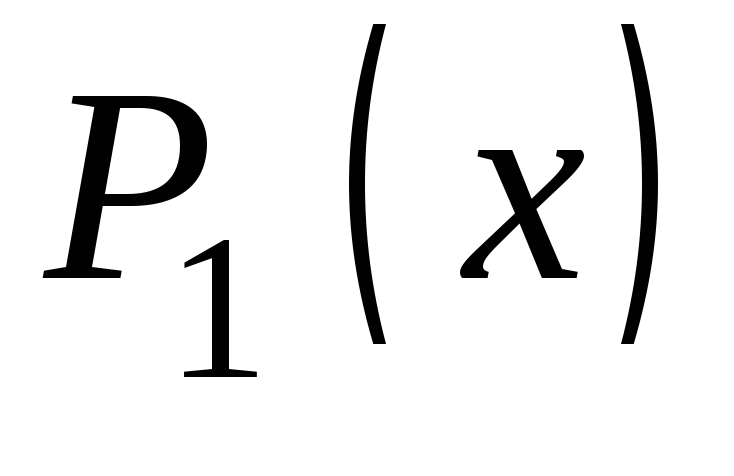
образовался остаток, равный «1» – признак
ошибки.
2 Исправление однократной ошибки
Исправление одиночной ошибки связано
с определением разряда, в котором
произошла ошибка. Это производится на
основании анализа остатков от деления
многочленов ошибок
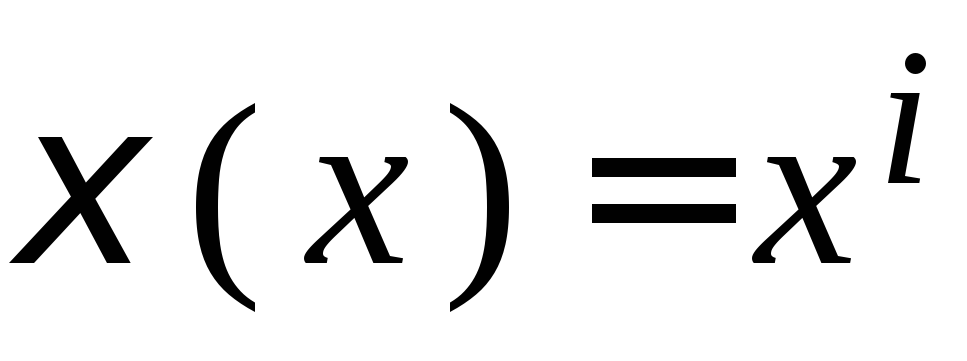
на неприводимый полином

.
Каждому остатку соответствует один из
разрядов кодовой комбинации, в которой
произошла ошибка. Чем больше остатков,
тем больше ошибок можно исправить.
Наибольшее число остатков дает
неприводимый полином
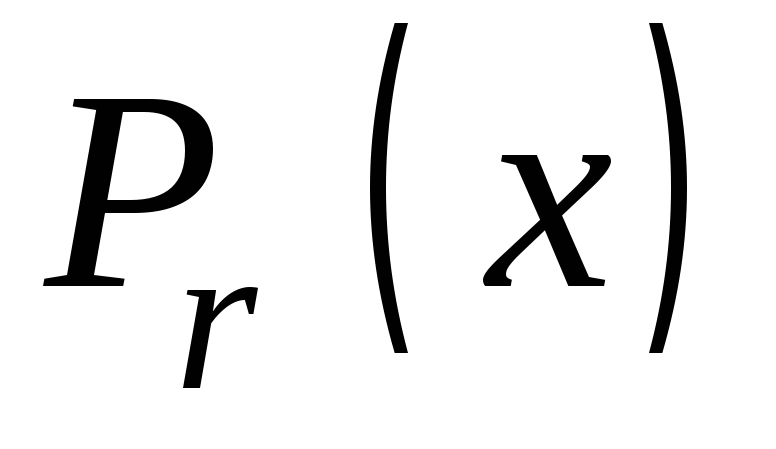
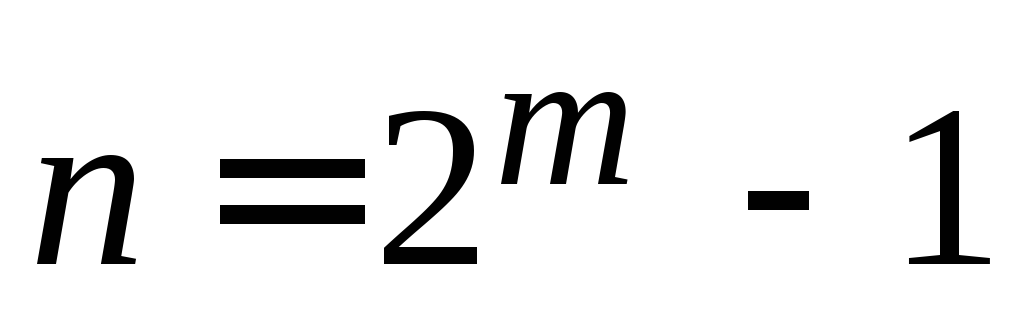
,
(5.18)
с кодовым расстоянием
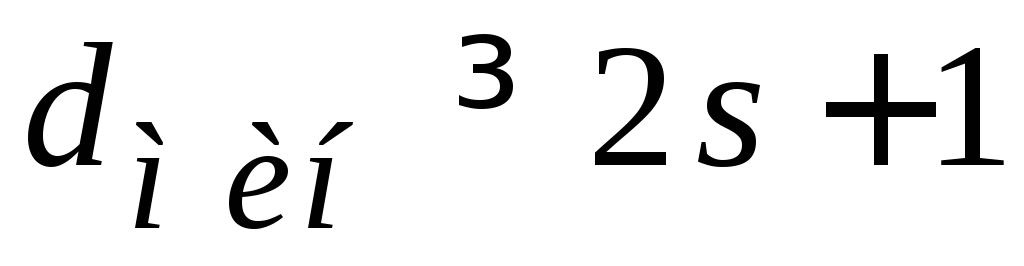
.
(5.19)
При этом число проверочных символов
удовлетворяет соотношению
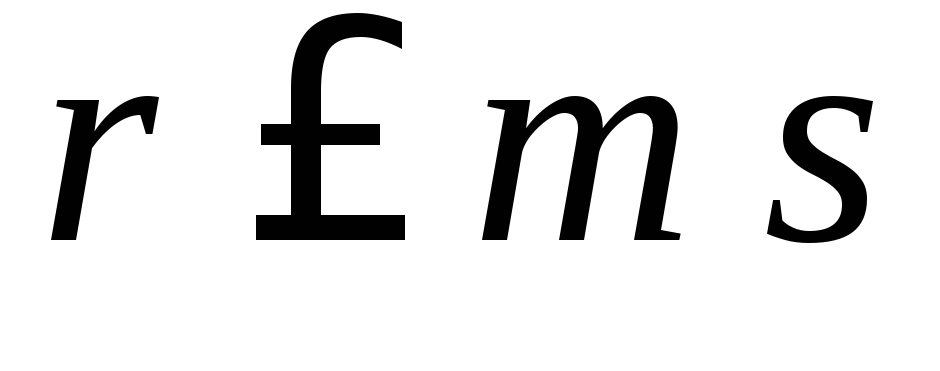
.
(5.20)
Соотношение между числом исправляемых
ошибок s, числом информационных
символов и числом проверочных символов
регулируется формулой (5.6).
В таблице 5.4 приведены значения числа
символов nв кодовой
последовательности в зависимости от
величиныm,обеспечивающие кодовое расстояниеd=3
при исправлении одиночной ошибки.
Для значенийn= 3, 7, 15 по
формуле (5.21) получены множества
неприводимых многочленов
Не
каждый многочлен даёт необходимое число
остатков. Например, при исправлении
однократной ошибки в 15-разрядном коде
необходимо 15 остатков , полученных от
деления кода ошибки на неприводимый
полином. Однако, если выбран полином
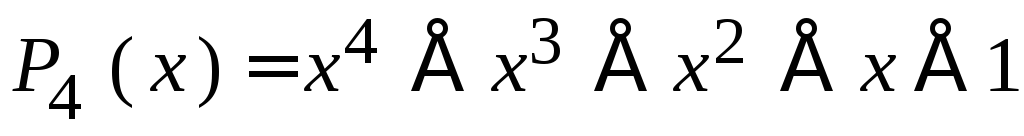
будет всего шесть остатков. В то же время
полином
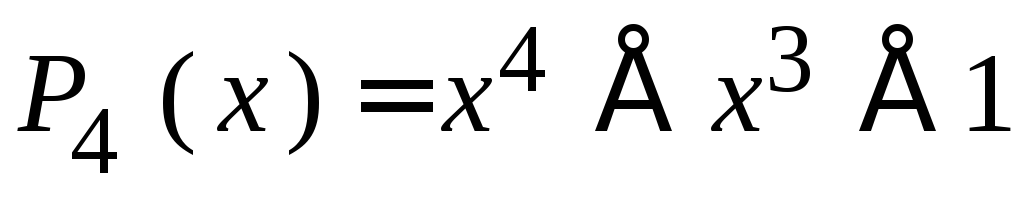
даёт 15 остатков. Двоичное значение
полинома
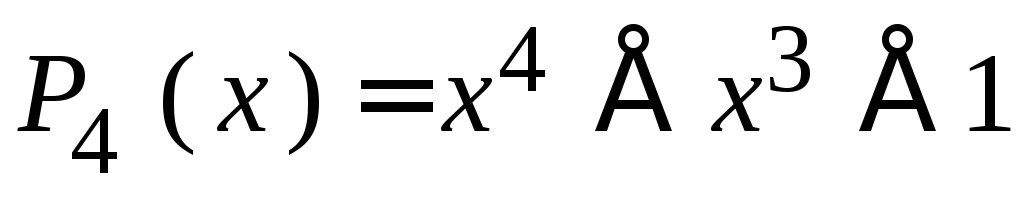
Образование циклического кода.n-разрядная кодовая
комбинация имеет вид
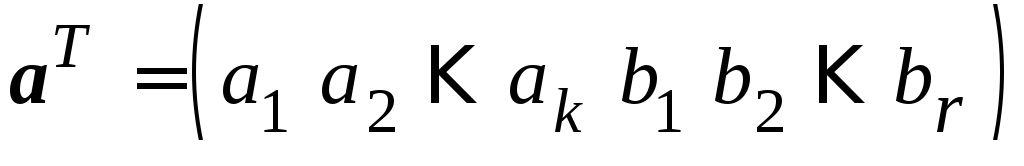
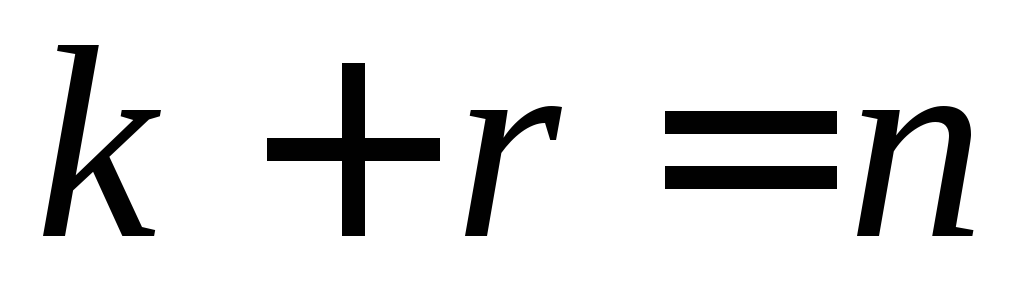
.
Положим, определеныk,rиn. Тогда известны неприводимый многочлен

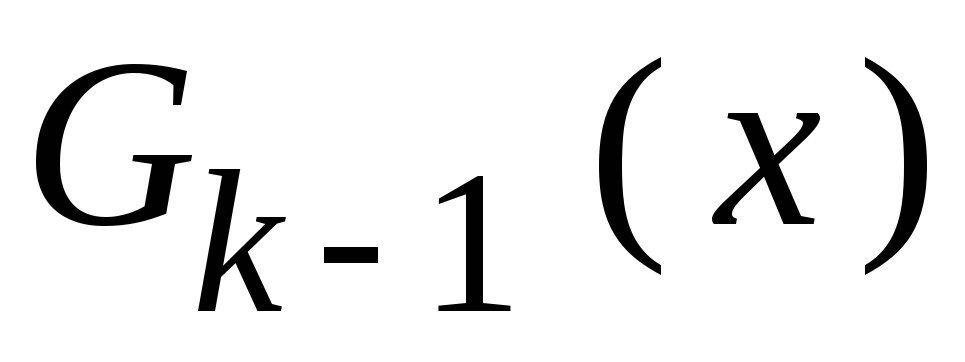
,
соответствующийk-разрядной
комбинации информационных символов
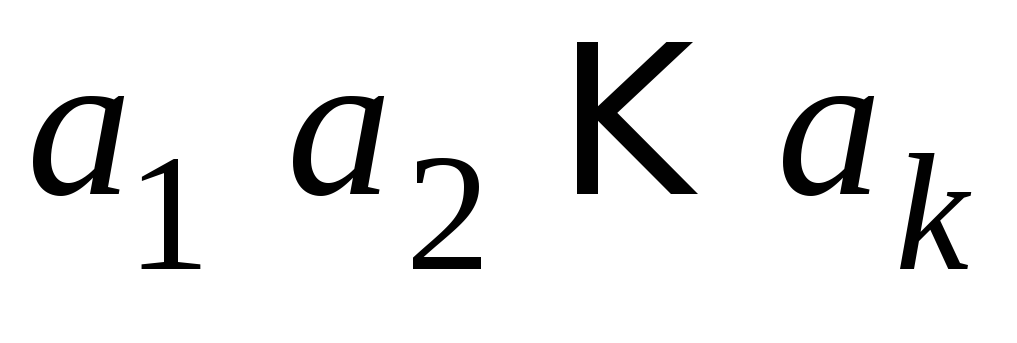
.
Необходимо определить проверочные
символы
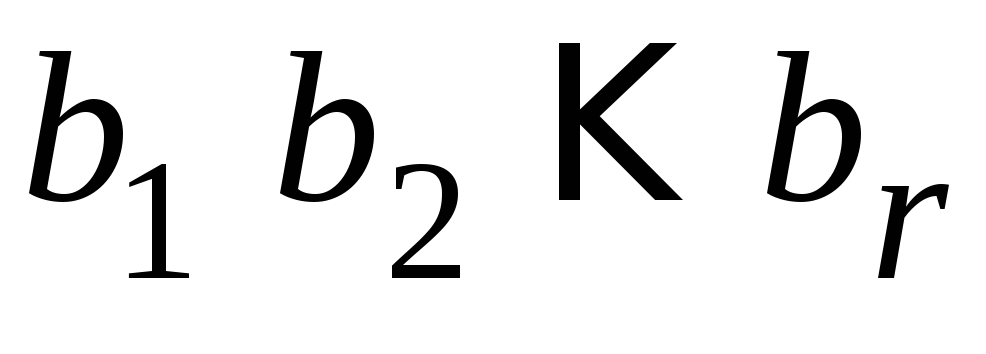
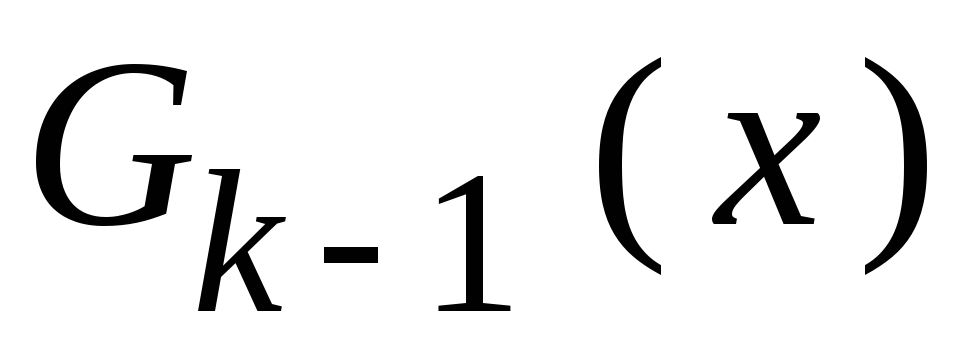
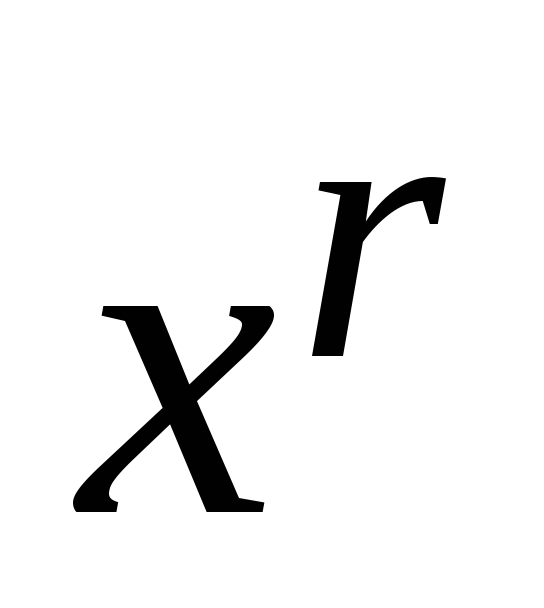
.
Это соответствует приписываниюrнулей справа в кодовой последовательности
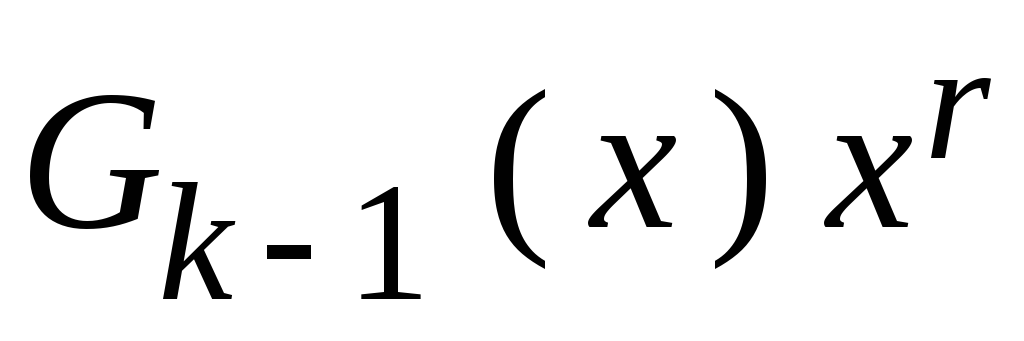
делится на неприводимый полином
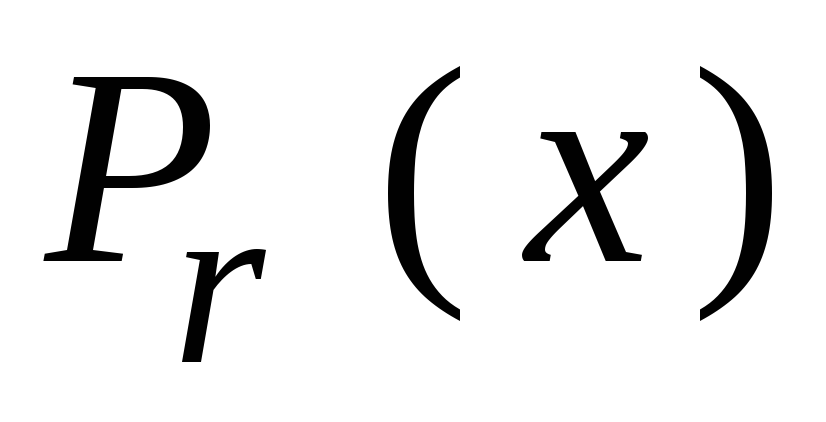
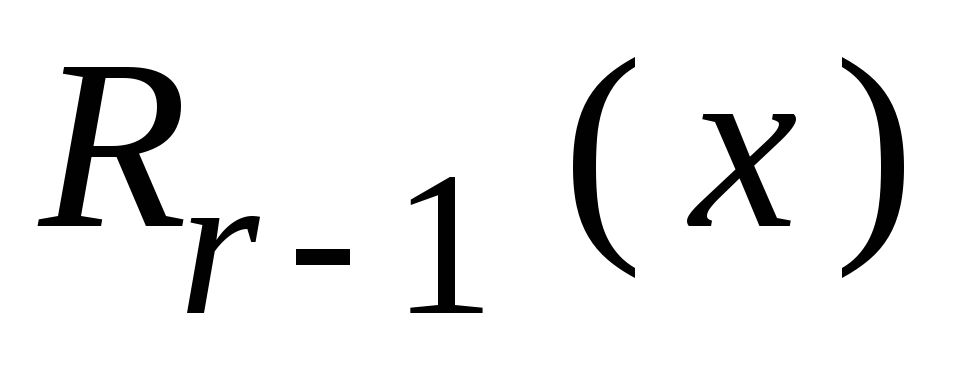
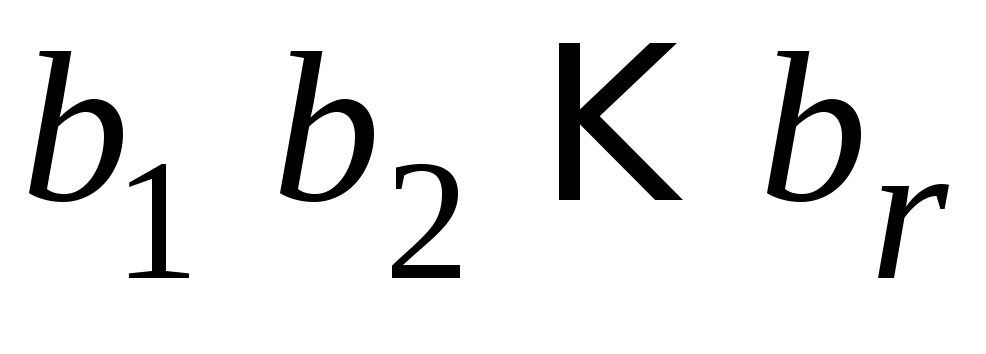
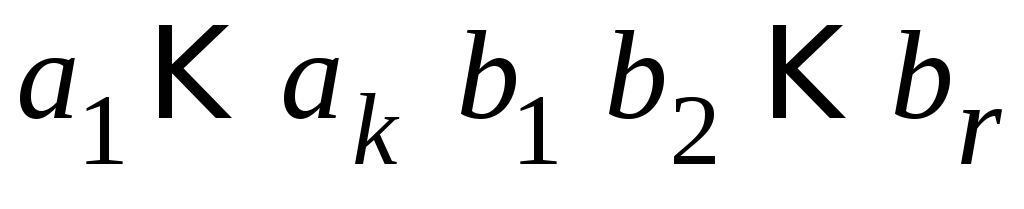
замещаются символами остатка. В результате
имеем многочлен
Полученный многочлен делится без остатка
на неприводимый многочлен. Действительно,
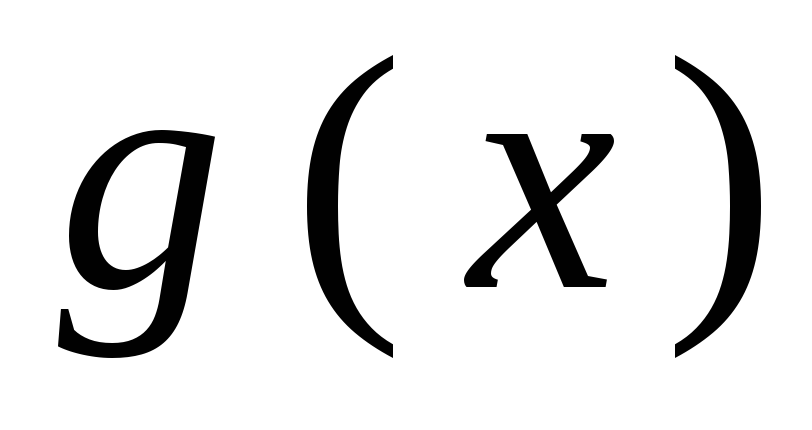
частное от деления
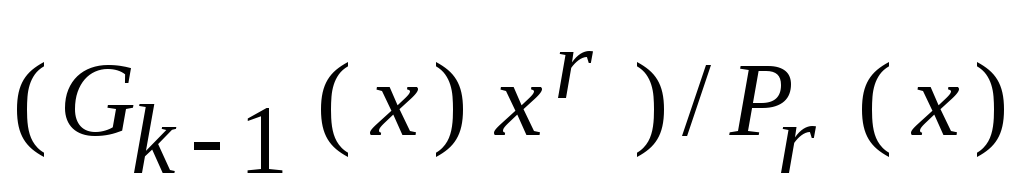
Если в одном из разрядов символ изменил
своё значение, остаток от деления
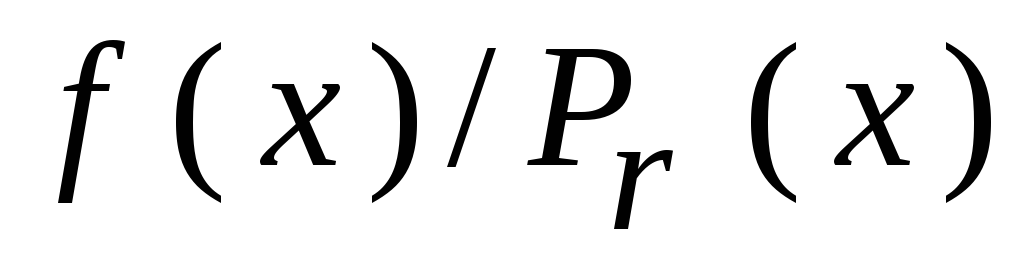
не равен нулю. Каждому ошибочному символу
в кодовой комбинации
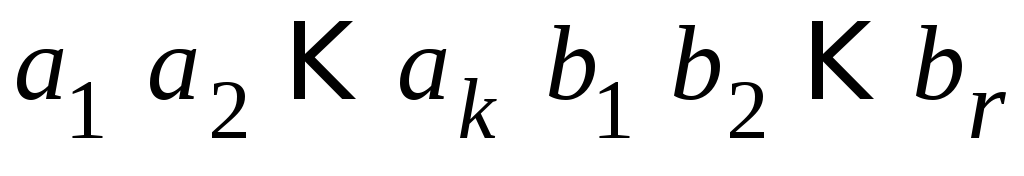
Пусть n= 7,k= 4,r= 3. Выберем полином
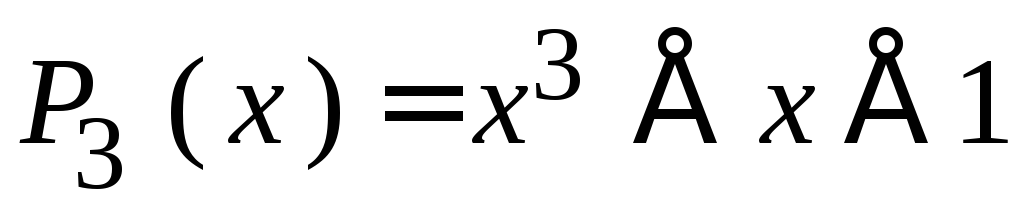
1011,
который дает 7 остатков. Положим,
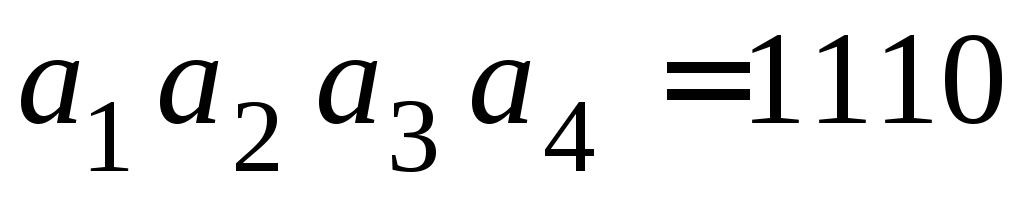
.
Неизвестными являются проверочные
символы
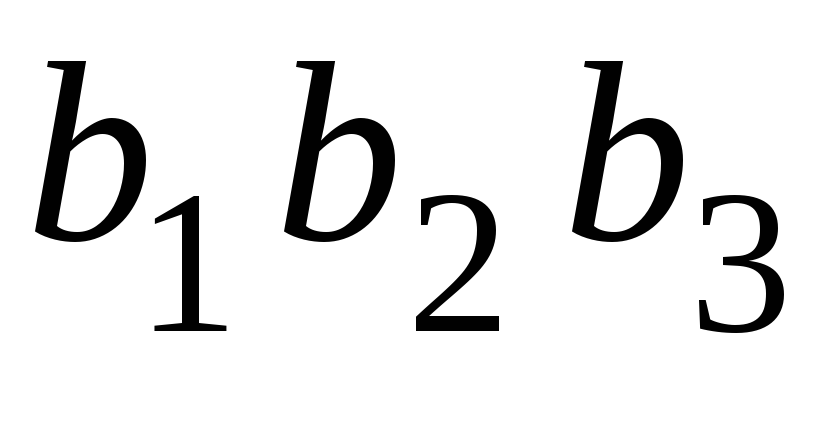
Определим полиномы и соответствующие
им коды
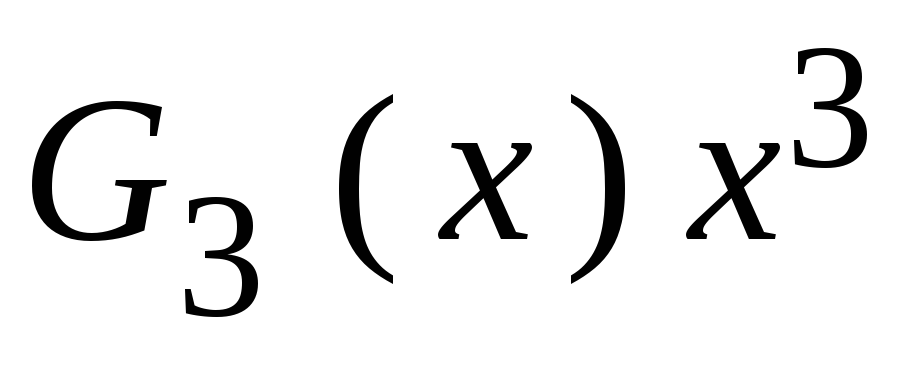
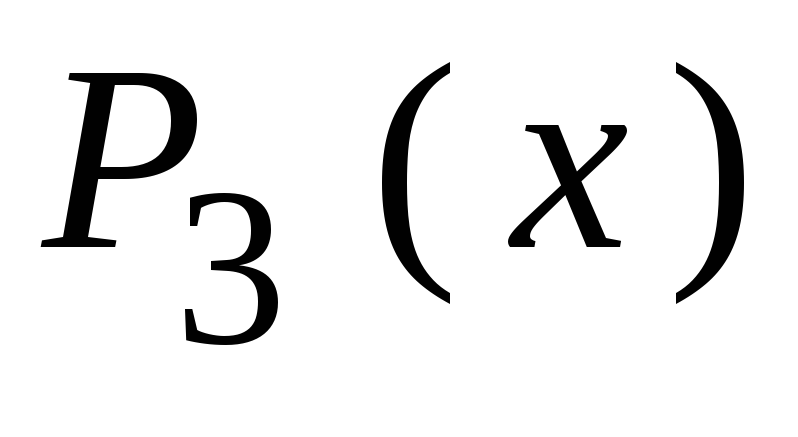
1011. Остаток от деления полинома
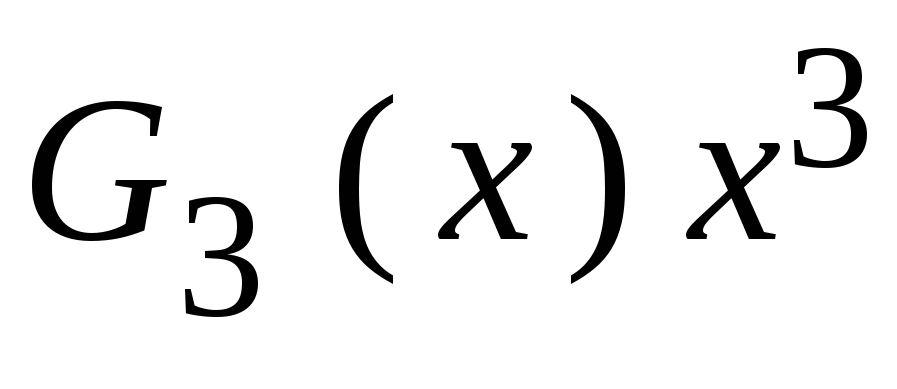
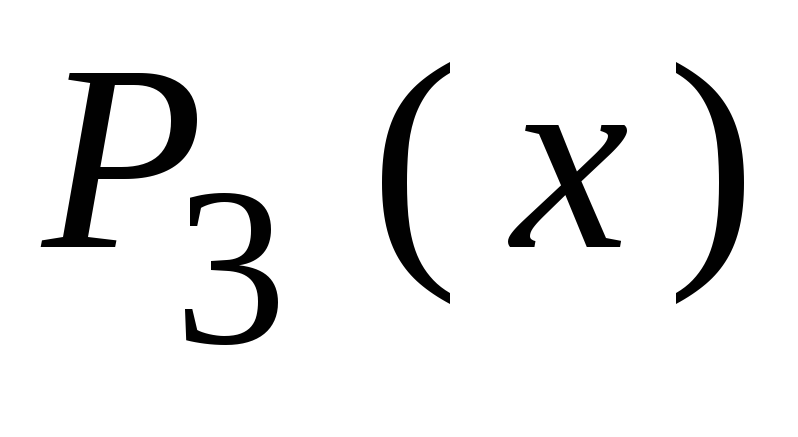
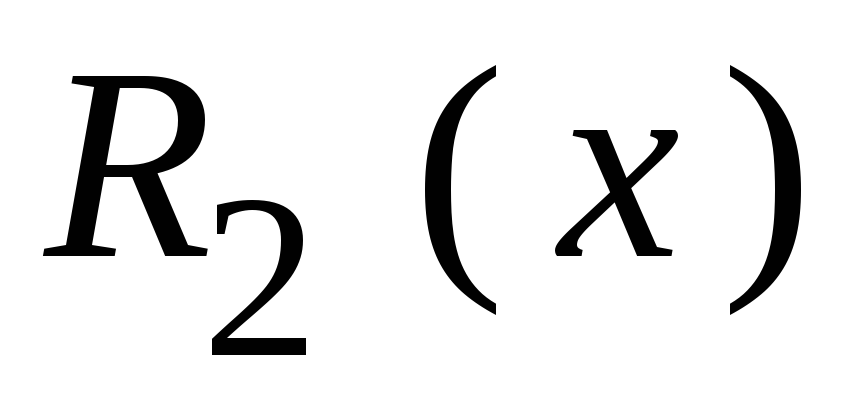
Заменим нули проверочной части кода
1110000 кодом остатка и получим закодированную
кодовую комбинацию 1110100, которому
соответствует полином вида
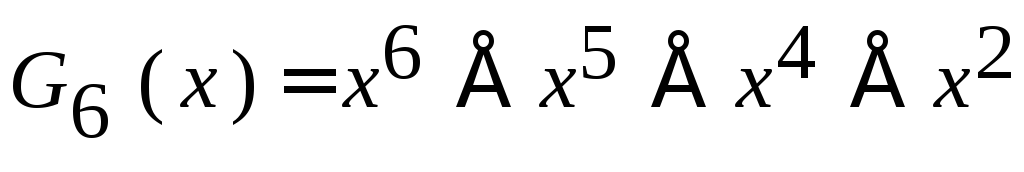
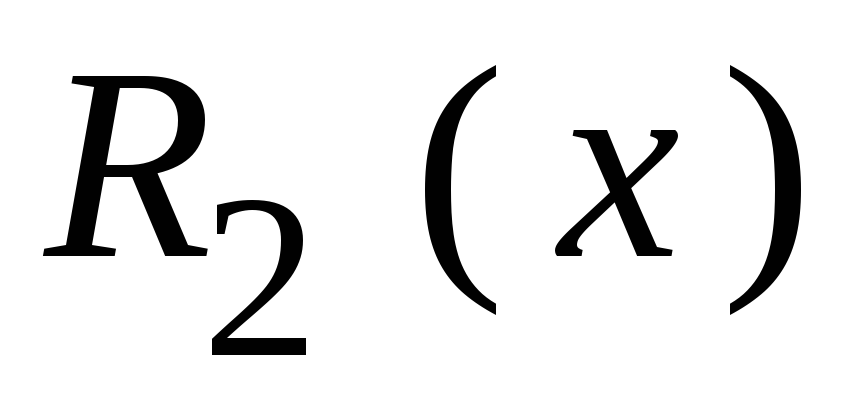
Исправление однократной ошибки. Для
исправления однократных ошибок определим
коды ошибок, соответствующие каждому
разряду кодовой комбинации. Заменяя
исправный символ в коде 1110100 ошибочным
и деля полученный код на код неприводимого
многочлена, получим код ошибки (синдром)
для соответствующего разряда. В результате
получится таблица 5.5. Если искажён
символ, скажем

,
то после деления кода с искажённым
символом на код неприводимого многочлена
получим синдром 011, что позволит
инвертировать символ

Исправление однократной ошибки возможно
несколькими методами. Используя методы
исправление однократной ошибки
систематическими кодами можно так же
создать проверочную матрицу, а по ней
записать проверочные уравнения. Другим
методом является метод, основанный на
свойствах записи циклических кодов и
весе однократной ошибки, равный единице.
Считается, множество кодов, составляющие
разрешённые комбинации , образовано с
помощью выбранного неприводимого
полинома и он остается неизменным во
время исправления однократной ошибки.
В зафиксированной кодовой комбинации
содержится однократная ошибка.При делении зафиксированной кодовой
комбинации на код образующего полинома
получается остаток. Если все разряды
кода не искажены, остаток равен нулю.
Искажение одного из символов приводит
к остатку, отличного от нуля. Анализ
остатка позволяет определить искажённый
символ. Ввиду того, что ошибка однократная
и надо найти разряд, в котором произошла
ошибка, то вес остатка

должен быть равен единице. Чтобы проверить
каждый разряд кода на наличие ошибки
производится поэтапно циклический
сдвиг влево на один разряд кодовой
комбинации. На каждом этапе осуществляется
деление сдвинутого кода на неприводимый
полином и определяется вес остатка

.
Процедура циклических сдвигов
останавливается, если вес остатка

=1.
Этот остаток служит индикатором того,
что последний разряд в сдвинутом коде
ошибочный и его надо инвертировать.
Инвертирование достигается суммированием
по модулю 2 сдвинутого кода с кодом
остатка.
Чтобы восстановить неискажённую кодовую
комбинацию производятся циклические
сдвиги вправо столько раз, сколько
производились циклические сдвиги влево.
Пример 5.6 Пустьn= 7,k= 4,r= 3. Выберем полином
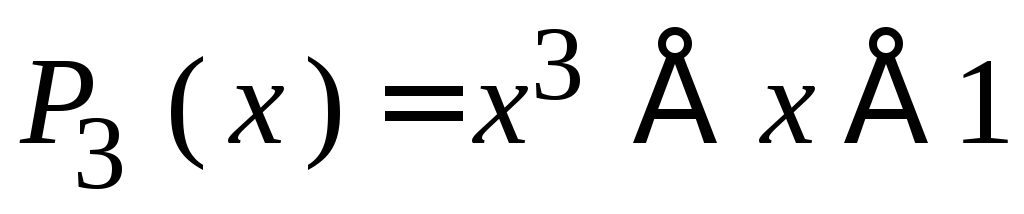
1011, который дает 7 остатков. Выберем из
множества разрешённых кодовых комбинаций
код 1110100 и внесём ошибку в 4-ый разряд
1111100. На рисунке 5.8 показана процедура
определения искажённого символа.
Разделив кодовую комбинацию с ошибкой
на неприводимый полином, убедимся, что
вес остаткаw
больше 1, рисунок 5.8 а. На рисунках 5.8 б,
5.8 в, 5.8 г показаны процедуры циклического
сдвига и получения остатков, больших
единицы. На рисунке 5.8.д демонстрируется,
после очередного циклического сдвига
и деления полученного кода на неприводимый
полином остаток равен единице,
следовательно вес остатка w=1.
Это значит последний сдвинутый символ
ошибочный. Чтобы исправить ошибочный
символ, последнюю кодовую комбинацию
сложим по модулю 2 с остатком, рисунок
5.8.е. Произведя последовательно 4 раза
циклический перенос вправо кодовой
комбинации с исправленным символом,
получим безошибочную кодовую комбинацию:
1001110
0100111, 1010011, 1101001,1110100.
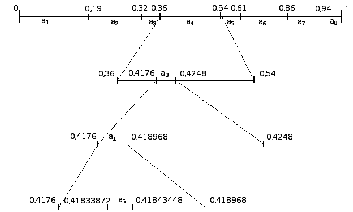
Изобразим интервалы на единичной
прямой:
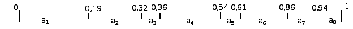
Передается: 4315 = a4a3a1a5
Начнем производить масштабирование:
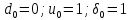
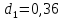
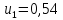
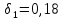

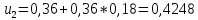
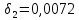
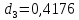
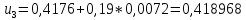
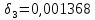
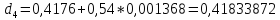
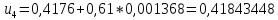
Найдем число архив:
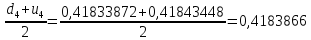
Вычислим количество разрядов, необходимых
для представления числа архива в двоичном
виде:
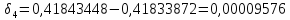
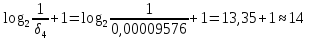
Закодируем число архив:
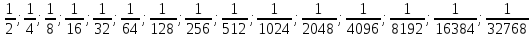
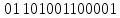
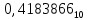
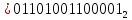
Задача №2. Нарисовать кодирующее
устройство и сформировать разрешенную
кодовую комбинацию циклического кода,
если задан производящий полиномP(x)
и кодовая комбинация, поступающая от
источника сообщенийQ(x).
Показать содержимое ячеек памяти кодера
на каждом такте.
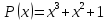
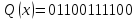
Сначала аналитически определим
разрешенную кодовую комбинацию,
соответствующую данной информационной.
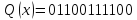
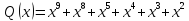
Далее действуем по алгоритму:
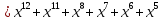
, гдеr– максимальная
степень производящего полинома.
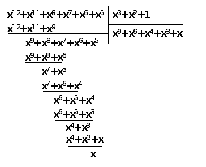
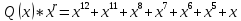
,
что в двоичном виде соответствует
комбинации 01100111100010 – это разрешенная
кодовая комбинация.
Для построения кодера необходимо: три
ячейки памяти (r=3), два сумматора
(r-1=3-1=2)
1) Число ячеек памяти равно степени
образующего полинома, т.е. r.
2) Число сумматоров на 1 меньше веса
образующего полинома.
3) Сумматор ставится после тех ячеек,
начиная с нулевой (её на схеме нет), для
которых существует соответствующий
ненулевой член в полиноме. После ячейки,
соответствующей старшему разряду,
сумматор не ставится.
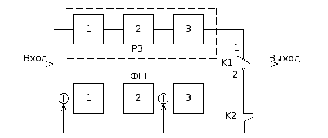
Рисунок 3. Схема кодера.
В начальный момент времени ключ K1в положении 2, ключK2разомкнут. Три такта идёт заполнение
ячеек ФПГ и РЗ. После третьего такта
ключи меняют своё положение, информационные
элементы уходят в канал, а в ФПГ идёт
деление на образующий полином. На 14
такте деление закончилось, ключи меняют
своё положение. После 14 такта проверочные
символы уходят в канал, а в это время
можно начинать передавать следующую
информационную комбинацию.
Таблица 1. Таблица состояний кодера.
Задача №3. Нарисовать декодирующее
устройство циклического кода с
исправлением однократной ошибки.
Определить наличие ошибки в кодовой
комбинации циклического кода, если
задан производящий полиномP(x)
и кодовая комбинация, поступающая на
вход декодера.
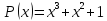
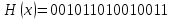
Представим кодовую комбинацию в виде
полинома:
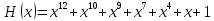
Определим наличие ошибок в кодовой
комбинации циклического кода:
Шаг 1. Делим вектор ошибки, соответствующий
старшему разряду на образующий полином
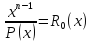

Шаг 2. Делим принятую КК на образующий
полином
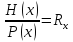
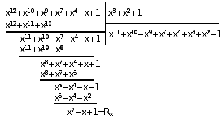
Так как R0(x)≠Rxто ошибки в первом разряде нет.
Шаг 3. Будем повышать степень на 1 и
продолжать деление пока Rxне совпадёт сR0(x)
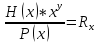
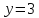
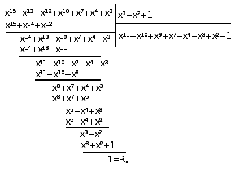

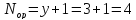
Делаем вывод, что ошибка в 4 разряде.
Изобразим декодирующее устройство
циклического кода с исправлением
однократной ошибки:
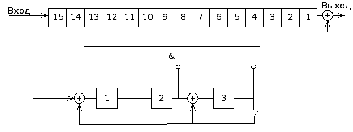
Рисунок 4. Схема декодера.
Исправленная кодовая комбинация:
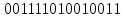
Коды, обнаруживающие трёхкратные ошибки
1)
Выбор числа корректирующих разрядов
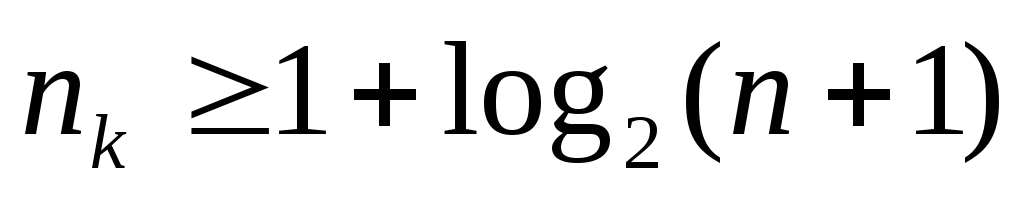
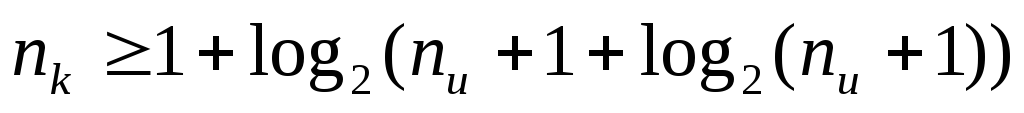
Значения
логарифма округряется
до целых чисел в большую сторону
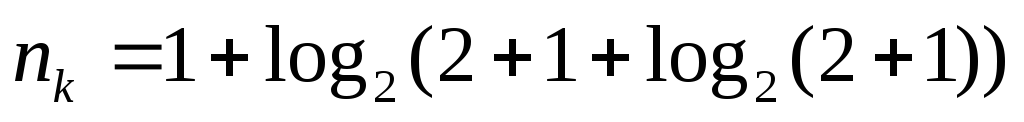
2)
Выбор образующего
многочлена. Он производится исходя из
следующих соображений: для обнаружения
трёхкратной ошибки надо иметь d0
= r + 1 = 3 + 1 = 4 степень
обратного многочлена должна быть больше
или равна четырём, т.е.
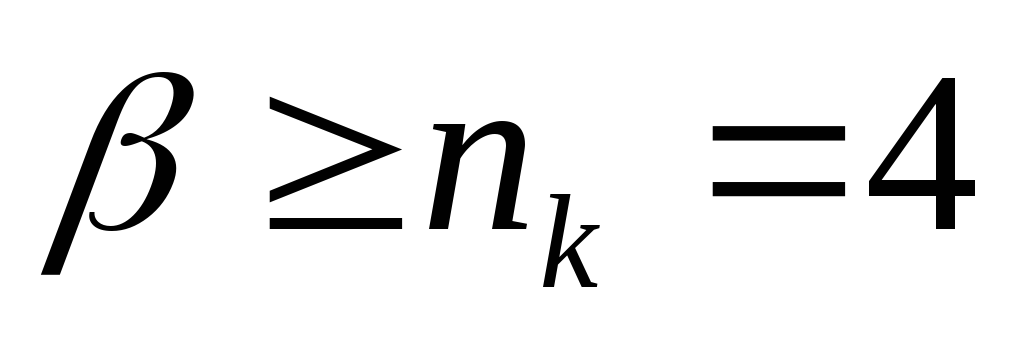
Этот
многочлен получают как произведение
многочлена степени (nk
– 1)т.е.
3, который
позволяет обнаруживать все двойственные
ошибки и многочлены первой степени (x
+ 1), который
обнаруживают любое количество нечётных
ошибок. Полученный многочлен унаследует
корректирующие свойства, т.е. он будет
обнаруживать одиночную и тройную ошибки,
используя корректирующие свойства
многочлена
x + 1 и будет
обнаруживать двойные ошибки, используя
свойства Шеннона, например x3
+
x2
+1.
M1
= x + 1
M3
= x3
+ x2
+ 1
M1
x M3
= (x + 1)( x3
+ x2
+ 1) = x4
+ x2
+ x +1 = k(x)
x3
+ x3
= 0 k(x) = 10111
x3
+ x3
+ x3
= x3
3)
Построение образующей матрицы
4)
Обнаружение ошибок производят по
остаткам от деления принятого кодового
вектора на образующий многочлен. Если
остатки есть, то принята ошибочная
комбинация.
Пример:
Строим код на
четыре комбинации
01
х к(х) = 01 x
10111 = 010111
10
х к(х) = 10 х 10111 = 101110


10101 Rx
= 10
обнаружена ошибка, надо повторить
передачу
Rx
= 1010 – есть остаток, следовательно,
посланная комбинация содержит ошибку.
k
= 110011 kx
= 10111
Rx
= 1110 – есть остаток,
следовательно, принятая комбинаяция
содержит ошибку. Какую ошибку мы не
указываем.
k
= 110111 kx
= 10111
Пример:
Построить образующий многочлен для
создания циклического кода, обнаруживающего
все трёхкратные ошибки при передаче
1000 сообщений.
1)
Определение количества параметров кода
nu
= log2
1000 = 10
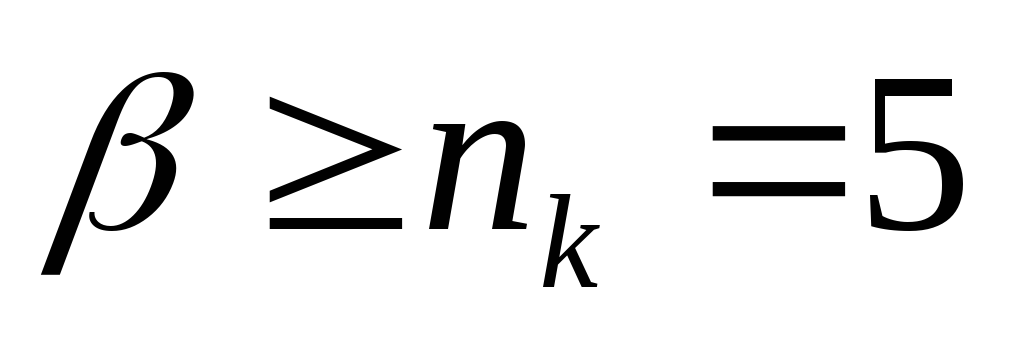
d0
= r + 1 = 4 – число ненулевых членов
образующего
многочлена
Из
таблицы нериводимых
многочленов, выбираем многочлен степени
nk
– 1
= 4, который
позволяет обнаруживать двойные ошибки.
M4
= x4
+ x + 1
k(x)
= M1
+ M4
= (x + 1)(x4
+
x + 1) = x5
+ x4
+ x2
+ 1
Передача
информации по дискретным каналам
связи 19
Соседние файлы в папке Lec
Принципы обнаружения и исправления ошибок в принятой кодовой комбинации циклического кода
Переданная кодовая комбинация двоичного циклического кода, представленная полиномом F(x), из-за искажений единичных элементов в каналах связи может быть принята с ошибками и иметь вид некоторого полинома Н(х). Если просуммировать по mod2 одноименные разряды F(х) и Н(х), то получим
где Е(х) – полином ошибок.
Разрядность полинома ошибок такая же, как и разрядность комбинации F(х) циклического кода. При этом ненулевые разряды в Е(х) указывают на ошибочные элементы в принятой кодовой комбинации Н(х). При отсутствии ошибок полином Е(х) состоит из одних нулей.
Принимая во внимание вышеприведенные обозначения, принятую кодовую комбинацию можно представить следующим образом:
Для обнаружения ошибок в принятой кодовой комбинации Н(х) следует разделить Н(х) на порождающий многочлен Р(х). Результат деления укажет на наличие или отсутствие ошибки в принятой кодовой комбинации Н(х). Если деление дает нулевой остаток, то ошибки отсутствуют или не обнаружены. Если же в результате деления полинома Н(х) на порождающий многочлен Р(х) остаток R’(х) отличен от нуля , то это означает что принятая кодовая комбинация Н(х) содержит ошибки (рис 2).
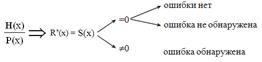
Рис.2. Схема выявления ошибок в принятой кодовой комбинации H(x)
Вид ненулевого остатка R’(x), называемого синдромом ошибки S(х), имеет однозначное соответствие с ошибочным разрядом и видом полинома однократной ошибки Е(х) для всех кодовых комбинаций Н(х) циклического кода. Например, для циклического кода (9,5) при заданном порождающем многочлене P(x)= x4 + x + 1 остаток R’(x) всегда будет иметь вид S(х)=0011, если ошибка возникла в пятом разряде входной кодовой комбинации, т.е. в младшем информационном разряде, независимо от вида переданной кодовой комбинации F(х).
Следует отметить, что остаток R’(x), получаемый при делении полинома Н(х), на порождающий многочлен Р(х), имеет такой же вид, как и остаток от деления Е(х) на Р(х), поскольку полином F(х) делится на Р(х) без остатка.
Кратность обнаруживаемых ошибок в принятой кодовой комбинации циклического кода определяется минимальным кодовым расстоянием dmin этого кода. Для циклического кода (9,5) значение dmin=3, что обеспечивает гарантированное обнаружение всех однократных и двукратных ошибок. Кроме того, код позволяет обнаруживать часть ошибок более высокой кратности, начиная с веса, равного dmin и более. Код не обнаруживает ошибки, если полином ошибки имеет вид разрешенной кодовой комбинации.
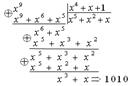
Номер такта, на котором в регистре-делителе возникает “особая” кодовая комбинация, указывает место ошибочного разряда в принятой кодовой комбинации Н(х). При считывании этой комбинации из буферного регистра ошибочный разряд должен быть исправлен (инвертирован).
Циклический код (9,5) гарантированно исправляет только однократные ошибки. Ошибки более высокой кратности код (9,5) не исправляет.
Заметим также, что деление полинома Н(х) на многочлен Р(х) и считывание информации из буферного регистра после 9го такта целесообразно осуществлять под действием “быстрых” тактовых импульсов. Это позволит без задержки принять из канала связи и обработать следующую кодовую комбинацию Н(х).
1. Структурная схема кодирующего и декодирующего устройства ( циклич. Коды ).

Решение. Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой
Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой комбинации, сумма которых по модулю два должна быть равна 0. Так, из матрицы (3.29) можно получить следующие уравнения проверок:
Естественно, что (3.27) и (3.30) полностью совпадают с той лишь разницей, что операции по (3.27) выполняются при кодировании для получения значений контрольных разрядов в каждой кодовой комбинации, а операции по (3.30) выполняются при декодировании для обнаружения и исправления ошибок.
Из анализа (3.30) видно, что a1 входит во все три уравнения, а2 – в первое и второе, а3 – в первое и третье, а4 – во второе и третье. Следовательно, искажение любого аi нарушит вполне определенные уравнения, т.е. сумма по модулю два в них будет рана не нулю, а единице. По тому, какие именно уравнения нарушены, можно определить, в каком разряде произошла ошибка, и восстановить его истинное значение.
Таким образом, результаты проверок дают кодовую комбинацию вида
, которую называют контрольной последовательностью или, чаще, синдромом. При
считается, что кодовая комбинация принята верно или произошла не обнаруживаемая ошибка. Если
, считается, что комбинация принята неверно, т.е. имеет место обнаружение ошибки. Если (n,k)-код используется только для обнаружения ошибок, то в теории кодирования доказывается, что при любой вероятности ошибочного приема кодового символа р£1/2 найдется код, для которого вероятность необнаруженной ошибки будет меньше вполне определенного значения
, а принимается
При выполнении проверок на приеме в соответствии с системой (3.30) получается
т.е. синдром R=110, нарушены первое и второе уравнения, в которые входит а2, следовательно, ошибка в разряде а2 и тогда исправляющий вектор Е=0010000, а исправленная кодовая комбинация
Пользуясь этим примером, обратим внимание на третью стоку образующей матрицы (3.26). В части этой строки, соответствующей единичной матрице, единица расположена на месте разряда, в котором произошла ошибка, а получившийся синдром R равен части этой же строки, входящей в дополняющую матрицу.
Обобщая, можно сказать, что при ошибке в разряде а4 синдром будет 011, при ошибке в разряде а3 – 101, при ошибке в разряде а1 – 111.
То же самое следует из проверочной матрицы этого кода (3.29), где первый столбец – синдром при ошибке в разряде а4 и т.д.
На основании любого из приведенных ранее описаний группового систематического кода (системы проверочных уравнений, образующей матрицы, проверочной матрицы) могут быть синтезированы функциональные схемы кодера и декодера такого кода.
Так, кодер (рис. 3.9) для кода из примера 3.8 должен содержать параллельный регистр, предназначенный для приема от источника и временного хранения четырех информационных разрядов, совокупность из трех трехвходовых сумматоров по модулю два, предназначенных для формирования значений контрольных разрядов, и параллельный семиразрядный регистр для промежуточного хранения сформированной кодовой комбинации, которая далее может быть последовательно передана в линию связи. Соединение входов сумматоров по модулю два с выходами первого регистра выполняются в соответствии с системой проверочных уравнений.
Сложность схемы декодера для такого кода будет зависеть от того, используется ли данный код в режиме обнаружения ошибки или в режиме исправления ошибки.
Для режима исправления ошибки в составе декодера (рис. 3.10) должны присутствовать следующие функциональные узлы:
– регистр для временного хранения принятой кодовой комбинации;
– устройство вычисления синдрома;
– дешифратор синдрома;
– устройство исправления ошибки;
– регистр для хранения исправленной информационной части комбинации.
Устройство вычисления синдрома представляет собой совокупность из трех сумматоров по модулю два, каждый из которых имеет по четыре входа, которые соединяются с выходами первого регистра в соответствии с системой проверочных уравнений, а выходы подключены к входам дешифратора синдрома. Дешифратор синдрома осуществляет преобразование синдрома в исправляющий вектор. Устройство исправления ошибок может быть реализовано в виде совокупности из четырех сумматоров по модулю два, каждый из которых имеет по два входа. Первые входы сумматоров соединяются с выходами информационных разрядов первого регистра, а вторые входы подключаются к соответствующим выходам дешифратора синдрома, а выходы соединены с соответствующими входами второго регистра.
Декодер, работающий в режиме обнаружения ошибок, проще, поскольку в нем отсутствует устройство исправления ошибок, а дешифратор синдрома может быть заменен одной схемой выявления ненулевого синдрома (рис. 3.11).
Рассмотренный алгоритм декодирования блоковых групповых линейных систематических (n, k)- кодов, называемый иногда синдромным, относится к классу алгебраических методов декодирования, в основе которых лежит решение системы уравнений, задающих расположение и значение ошибки.
Для декодирования этих кодов могут использоваться и неалгебраические методы, использующие простые структурные понятия теории кодирования, которые позволяют найти комбинации ошибок более прямым путем. Одним из таких алгоритмов является декодирование по максимуму правдоподобия.
Этот метод основывается на том предположении, что если все кодовые комбинации передаются по двоичному симметричному каналу с равной вероятностью, то наилучшим решением при приеме является такое, при котором переданной считается кодовая комбинация, отличающаяся от принятой в наименьшем числе разрядов.
В связи с этим алгоритм максимального правдоподобия реализуется в виде следующей последовательности действий:
1) принятая кодовая комбинация Y суммируется по модулю два последовательно со всеми кодовыми комбинациями кода Xi , в результате каждого суммирования вычисляются векторы ошибок ei = Y+Xi ,
2) подсчитывается число di единиц в каждом из векторов ошибки ei.
3) та из Xi, для которой di минимально, считается переданной кодовой комбинацией.
Для некоторых систематических (n,k)-кодов неравенство (3.23)
превращается в строгое равенство
Для таких кодов можно записать
. (n,k)-коды вида
называются кодами Хэмминга..
Образующая матрица кода Хэмминга (7,4) приведена ранее (3.26). Образующие матрицы кодов больших размерностей строятся аналогично. Уравнение (3.31) имеет целочисленные решения при k=0,1,4,11,26,57,120, . . , что дает соответствующие коды Хэмминга (3,1), (7,4), (15,11), (31,26), (63,57), (127,120),. . . . Коды Хэмминга относятся к немногим известным т.н. совершенным кодам.
С учетом данных ранее определений кодового пространства и кодового расстояния представим некоторый код в виде сфер с центрами во всех разрешенных кодовых комбинациях. Все сферы имеют одинаковый целочисленный радиус. Будем увеличивать его, оставляя целочисленным, до тех пор, пока сферы не соприкоснутся. Значение этого радиуса равно числу исправляемых кодом ошибок. Этот радиус называется радиусом сферической упаковки кода.
Теперь позволим этому радиусу увеличиваться до тех пор, пока каждая точка кодового пространства не окажется внутри хотя бы одной сферы. Такой радиус называется радиусом покрытия кода. Радиус упаковки и радиус покрытия кода могут совпадать.
Код, для которого сферы некоторого одинакового радиуса вокруг кодовых слов, не пересекаясь, покрывают все кодовое пространство, называются совершенными. Совершенный код удовлетворяет границе Хэмминга с равенством. Код Хэмминга, имеющий длину
, является совершенным.
Код, у которого сферы радиуса t вокруг каждого кодового слова не пересекаются и все кодовые слова, не лежащие внутри какой-либо из этих сфер, находятся на расстоянии t+1 хотя бы от одного кодового слова, называется квазисовершенным. Квазисовершенные коды встречаются чаще, чем совершенные. Если для заданных n и k существует квазисовершенный и не существует совершенного кода, то для этих n и k не существует кода с большим, чем у квазисовершенного, кодовым расстоянием.
Систематические коды, в том числе и код Хэмминга, допускают различные преобразования, которые, порождая новые коды, тем не менее, не выводят их из класса линейных групповых кодов.
К числу наиболее часто используемых преобразований кодов относят укорочение и расширение кодов.
Укорочение кода состоит в уменьшении длины кодовых комбинаций путем удаления лишних информационных разрядов. Если код задан порождающей матрицей, то это приводит к уменьшению обоих размеров порождающей матрицы на одно и то же число. Так, например, как упоминалось ранее, коды Хэмминга с d=3 могут быть построены с вполне определенным сочетанием n и k. Как поступить в том случае, если требуется код Хэмминга с d=3, для передачи информации достаточно k=8, а на длину кодовой комбинации наложено ограничение n<15. Для выполнения этих требований можно выбрать код Хэмминга (15,11) и прибегнуть к его укорочению. Укорочение производится за счет удаления требуемого числа лишних информационных разрядов, обычно это первые слева разряды. В образующей матрице кода (15,11) полагаются равными нулю столько столбцов слева, сколько разрядов надо удалить, после чего вычеркиваются нулевые столбцы и строки с полностью нулевыми строками единичной матрицы. Относительно проверочной матрицы операция укорочения выражается в удалении соответствующего количества первых слева столбцов, так как число строк проверочной матрицы, равное числу контрольных разрядов, остается неизменным при укорочении. Для приведенных значений k=8 и n<15 из кода (15,11) нужно удалить три лишних информационных разряда, в результате чего получится укороченный код (12,8), который также называется кодом Хэмминга.
Расширение кода состоит в увеличении длины кодовых комбинаций за счет введения новых контрольных разрядов, что приводит к увеличению большего размера порождающей матрицы, и, естественно, к увеличению d, т.е. повышению корректирующих способностей. В качестве примера можно привести расширенный код Хэмминга (8,4) с d=4. Этот код образуется путем добавления к каждой кодовой комбинации кода Хэмминга (7,4) еще одного контрольного разряда, значение которого определяется как сумма по модулю два всех остальных разрядов кодовой комбинации, т.е. общая проверка на четность всей кодовой комбинации. При декодировании комбинаций этого кода возможны следующие варианты: 1) ошибок нет. Это показывает как общая проверка на четность, так и равенство нулю синдрома. 2) одиночная ошибка. Общая проверка на четность указывает на наличие ошибки, а по синдрому находится номер искаженного разряда и ошибка в нем исправляется. Нулевой синдром в этом случае указывает на наличие ошибки в дополнительном разряде, т.о. имеет место режим исправления ошибок. 3) две ошибки. Общая проверка на четность указывает на отсутствие ошибок, ненулевой синдром – на их наличие, причем значение синдрома указывает на разряд в котором якобы произошла ошибка, однако в этом случае ее не следует исправлять, а лишь констатировать наличие двух ошибок, т.о. реализуется режим обнаружения ошибок.
Рассмотренные преобразования (укорочение и расширение) можно использовать для модификации известных кодов, чтобы сделать их подходящими для каких-либо конкретных приложений, а также для получения новых классов хороших кодов.
