Итак. Задача. Использовать код Хэмминга для двоичного сообщения, длина слова у которого составляет 16 бит. Исходное сообщение возьмём такое «0100010000111101». То есть в слове 16 «букв», каждая из которых может принимать значение либо «0», либо «1».

Рассмотрим (7,4)-код Хемминга, являющийся классической иллюстрацией простейших кодов с исправлением ошибок. Пусть m = (m0, m1, m2, m3) будет тем сообщением, или информационной последовательностью, которую нужно закодировать. Порождающая матрица G для (7, 4)-кода Хемминга имеет вид

Тогда символы соответствующего кодового слова определяются следующим образом :

Например, пусть m = ( 1 0 1 1 ) , тогда соответствующее кодовое слово будет иметь вид U = ( 1 0 1 1 1 0 0 ). Или другой пример: пусть m = ( 1 0 0 0 ), тогда U = ( 1 0 0 0 1 1 0 ).
На основании порождающей матрицы G(7,4) легко реализовать схему кодирования для рассматриваемого (7,4)-кода Хемминга (рис.

Рис. Структурная схема кодера для (7, 4)-кода Хэмминга
Кодер работает точно так же, как и при простой проверке на четность, но теперь выполняет не одну общую, а несколько частичных проверок, формируя, соответственно, несколько проверочных символов.
Для описания возникающих в канале ошибок Коржик В. и др. Расчет помехоустойчивости систем передачи дискретных сообщений. – М. : Радио и связь, 1981. – С. 87 – 99. используют вектор ошибки, обычно обозначаемый как e и представляющий собой двоичную последовательность длиной n с единицами в тех позициях, в которых произошли ошибки. Так, вектор ошибки e = ( 0 0 0 1 0 0 0 ) означает однократную ошибку в четвертой позиции (четвертом бите), вектор ошибки e = ( 1 1 0 0 0 0 0 ) – двойную ошибку в первом и втором битах и т.
Тогда при передаче кодового слова U по каналу с ошибками принятая последовательность r будет иметь вид
r = U + e.
Приняв вектор r , декодер сначала должен определить, имеются ли в принятой последовательности ошибки. Если ошибки есть, то он должен выполнить действия по их исправлению.
Чтобы проверить, является ли принятый вектор кодовым словом, декодер вычисляет (n-k)-последовательность, определяемую следующим образом:

Здесь НТ – проверочная матрица. При этом r является кодовым словом тогда, и только тогда, когда S = (00. 0), и не является кодовым словом данного кода, если S ненулевой. Следовательно, S используется для обнаружения ошибок, ненулевое значение S служит признаком наличия ошибок в принятой последовательности. Поэтому вектор S называется синдромом принятого вектора r.
Некоторые сочетания ошибок, используя синдром, обнаружить невозможно Тепляков И. , Рощин Б. Радиосистемы передачи информации. – М. : Радио и связь, 1982. – С. 201. Например, если переданное кодовое слово U под влиянием помех превратилось в другое действительное кодовое слово V этого же кода, то синдром равен 0. В этом случае декодер ошибки не обнаружит и, естественно, не попытается ее исправить. Сочетания ошибок такого типа называются необнаруживаемыми. При построении кодов необходимо стремиться к тому, чтобы они обнаруживали наиболее вероятные сочетания ошибок.
Для рассматриваемого линейного блочного систематического (7,4)-кода Хемминга синдром определяется следующим образом:
пусть принят вектор r = ( r0 , r1 , r2 , r3 , r4 , r5 , r6), тогда

Основываясь на полученных соотношениях, можно легко организовать схему для вычисления синдрома. Для (7,4)-кода Хемминга она приведена на рис.
Покажем теперь, как можно использовать синдром принятого вектора не только для обнаружения, но и для исправления ошибок.

Рис. Структурная схема определения синдрома для (7, 4)-кода Хэмминга

Таким образом, синдром принятой последовательности r зависит только от ошибки, имеющей место в этой последовательности, и совершенно не зависит от переданного кодового слова. Задача декодера, используя эту зависимость, определить элементы (координаты) вектора ошибок. Найдя вектор ошибки можно восстановить кодовое слово.
На примере одиночных ошибок при кодировании с использованием линейного блочного (7, 4)-кода покажем, как вектор ошибки связан с синдромом, и как, имея синдром, локализовать и устранить ошибки, возникшие при передаче.
Найдем значения синдрома для всех возможных одиночных ошибок в последовательности из семи символов. Все возможные для (7, 4)-кода одиночные ошибки и соответствующие им векторы синдрома приведены в табл.
Из этой таблицы видно, что существует однозначное соответствие между сочетанием ошибок (при одиночной ошибке) и его синдромом, то есть, зная синдром, можно совершенно однозначно определить позицию кода, в которой произошла ошибка.

Например, если синдром, вычисленный по принятому вектору, равен ( 111 ), это значит, что произошла одиночная ошибка в третьем символе, если S = ( 001 ) – то в последнем, и т. Если место ошибки определено, то устранить ее уже не представляет никакого труда.
Полная декодирующая схема для (7, 4)-кода Хемминга, использующая синдром вектора r не только для обнаружения, но и для исправления ошибок, приведена на рис.
А теперь посмотрим, что произойдет, если в принятой последовательности будет не одна, а, например, две ошибки. Пусть ошибки возникли во второй и шестой позициях e = ( 0100010 ). Соответствующий синдром определится как

Однако синдром S = ( 001 ) соответствует также и одиночной ошибке в седьмой позиции ( e6 ). Следовательно, наш декодер не только не исправит ошибок в позициях, в которых они произошли, но и внесет ошибку в ту позицию, где ее не было. Таким образом, видно, что (7, 4)-код не обеспечивает исправления двойных ошибок, а также ошибок большей кратности. Это, однако, обусловлено не тем, каким образом производится декодирование, а свойствами самого кода Мордухович Л. , Степанов А. Системы радиосвязи (курсовое проектирование). – М. : Радио и связь, 1987. – С.

Рис. Структурная схема декодера для (7, 4)-кода Хэмминга
(7, 4)-код Хэмминга имеет минимальное кодовое расстояние dmin = 3, а, следовательно, позволяет исправлять лишь одиночные ошибки.
Обнаружение ошибок в кодах Хемминга
Ошибка на выходе из канала связи может быть обнаружена и исправлена так (для построенного кода – не больше одной в каждом элементарном коде). Номер позиции S (записанный в двоичной системе), в которой произошла ошибка, определяется так:
где Si определяется по формулам (4) для элементарного кода, полученного на выходе канала связи. Если ошибки нет, то Si = 0 и общий результат S = 0.
Пример 1: Пусть на вход канала связи поступил элементарный код 0110011 (т. е закодировано **1*011 (поз. 3,5,6,7– информационные, а контрольные члены заменены * )). На выходе получено 0110001 (искажен 6–й член элементарного кода). Вычислим S.
S1 = b1 + b3+ b5 + b7 = 0 + 1 + 0 + 1 = 0 (mod 2),
S2= b2 + b3+ b6 + b7 = 1 + 1 + 0 + 1 = 1 (mod 2),
S3= b4 + b5 + b6 + b7 = 0 + 0 + 0 + 1 = 1 (mod 2).
S= 1 1 0 = 6 (в десятичной системе).
Пример 2:Пусть на выходе получено 0111011 (искажен 4–й (контрольный) член элементарного кода).
S2= b2 + b3+ b6 + b7 = 1 + 1 + 1 + 1 = 0 (mod 2),
S3= b4+ b5 + b6 + b7 = 1 + 0 + 1 + 1 = 1 (mod 2).
S= S3 S2 S1=1 0 0 = 4 (в десятичной системе).
Тогда восстановленное сообщение имеет вид: 0110011, а исходное сообщение – 1011(удалены контрольные члены, выделенные цветом)
После получения закодированного сообщения происходит его разбивка на элементарные коды, вычисление для каждого кода Sи в случае его неравенства 0 – корректировка соответствующего информационного члена (если S указывает на контрольный член, то корректировка не нужна). После удаления всех контрольных членов получаем исходное сообщение.
Алфавитное кодирование с минимальной избыточностью
Пусть задано алфавитное кодирование со схемой å
Теорема 1 Если алфавитное кодирование со схемой å обладает свойством взаимной однозначности, то выполняется следующее неравенство (неравенство Макмиллана):
Нельзя построить схему алфавитного кодирования, обладающую свойством взаимной однозначности, если неравенство (3. 5) нарушено.
3 Теоремы 1 и 3 не дают полного алгоритма построения схемы алфавитного кодирования, обладающей свойством взаимной однозначности (если выполняется неравенство 5 – такая схема существует и можно продолжать ее построение, используя другие свойства и теоремы).
где li = l (Bi) (6)
Если имеется статистика о вероятности появления символов входного алфавита
Эта характеристика может изменяться как при переходе от одной схемы кодирования к другой, так и при изменении вероятностных характеристик источника сообщений. Введем для фиксированного источника сообщений характеристику l*.
l* = (8)
В формуле (8) минимум берется по всем схемам кодирования å, обеспечивающим свойство взаимной однозначности.
Оценим интервал значений lср для схем кодирования å, обеспечивающих свойство взаимной однозначности.
Определение. Коды, определяемые схемой å с lср = l*, называют кодами с минимальной избыточностью, или кодами Хаффмана.
Такие коды дают в среднем минимальное увеличение длин слов при кодировании сообщений заданного источника. Представляет практический интерес задача построения таких кодов (схем кодирования) для источника сообщений с фиксированными характеристиками (в силу вышеизложенного можно ограничиться рассмотрением только схем кодирования, обладающих свойством префикса).
Построение кодов Хаффмана
Обобщим представление об алфавитном кодировании. Каждой схеме алфавитного кодирования å со свойством префикса можно поставить в соответствие кодовое дерево (связный ациклический неориентированный граф), которое является частью обобщенного кодового дерева. Обобщенное кодовое дерево строится так:
Ø выбирается начальная вершина (нулевой ярус дерева m = 0 );
Ø из каждой вершины первого яруса снова выходит пучок ребер, количество которых равно q, и которые обозначены элементами алфавита O (второй ярус дерева m = 2 );
Ø аналогично строятся третий, четвертый и т. ярусы;
Кодовое дерево для конкретной схемы кодирования со свойством префикса будет являться частью обобщенного дерева, причем каждому элементарному коду должна соответствовать концевая вершина этого дерева, а начальные вершины должны совпадать.
С использованием вершин первого яруса как концевых, можно закодировать максимум 3х –символьный входной алфавит, второго 9ти – символьный и т. Если r в точности равно q m, то кодом Хаффмана будет схема кодирование элементарными кодами длины m из m–го яруса кодового дерева. Элементарные коды Bi записываются как цепи, соединяющие начальную вершину кодового дерева с каждой из вершин m–го яруса.
Более сложный случай, когда
(для конкретного значения r всегда можно подобрать целое m, удовлетворяющее этому неравенству).
Общие принципы поиска кода (схемы кодирования) с минимальной избыточностью:
§ для построения элементарных кодов использовать только m и m+1 ярусы кодового дерева;
§ переходить на m+1 ярус можно только после исчерпания всех возможностей m– го яруса.
Для реализации этого алгоритма необходимо представить r в виде:
r = (q m–n)+ q ×n – t, (12)
где n – число вершин в кодовом дереве яруса m, которые ветвятся в m+1 ярус;
t число вершин m+1 яруса, не задействованных при построении схемы кодирования ( t < q).
Формула для определения l* будет иметь следующий вид:
Если имеется информация о вероятности появления символов входного алфавита
Лемма 1 Для кода с минимальной избыточностью из условия pj < pi следует, что
l j ³ lj.
Следствие. В кодовом дереве для кода с минимальной избыточностью вероятности, приписанные концевым вершинам из m–го яруса не меньше, чем вероятности, приписанные концевым вершинам из m +1–го яруса.
Определение. Неконцевая вершина кодового дерева называется насыщенной, если ее порядок ветвления равен q. Кодовое дерево называется насыщенным, если в нем насыщены все неконцевые вершины, за исключением, быть может, одной, лежащей в предпоследнем ярусе, и порядок ветвления этой вершины равен qо, где 2 ≤ qо < q (если в насыщенном дереве нет исключительной вершины, то будем считать, что qо = q и роль исключительной может играть любая вершина из предпоследнего яруса). При решении задач для определения порядка ветвления исключительной вершины находят остаток от деления r / (q –1) и назначают qо в соответствии с (14):
Лемма 2 Среди кодов с минимальной избыточностью существует код, кодовое дерево которого является насыщенным.
Теорема 3 Среди кодов с минимальной избыточностью существует приведенный код (схема кодирования), причем qо определяется в соответствии с (14).
Приведенным будем называть такое кодовое дерево, в котором концевым вершинам, выходящим из qо приписаны минимальные вероятности.
Описание алгоритма поиска кода с минимальной избыточностью (кода Хаффмана) для случая алфавитного кодирования, если имеется информация о вероятности появления символов входного алфавита.
1 Определить qо по формуле (14).
3 Для последнего свернутого по п. 2 списка строится одноярусное кодовое дерево (из начальной вершины выходит q ребер, каждому из которых приписывается буква алфавита O, а каждой вершине 1–го яруса вероятности из последнего свернутого списка).
4 Построить 2–й, 3–й и другие ярусы кодового дерева, на которых развернуть просуммированные вероятности последнего, предпоследнего и т. списков(вершины, которым приписаны вероятности букв входного алфавита на любом ярусе, становятся концевыми); в результате таких действий получим кодовое дерево, в котором r концевых вершин и каждой из которых приписана вероятность pj. Выписав цепи из нулевой вершины к концевым (перечень ребер), получим схему кодирования с минимальной избыточностью.
Пример1: Построить код с минимальной избыточностью (код Хаффмана) для следующих исходных данных:
2 Упорядоченный список вероятностей 1 (7 чисел):
0,26; 0,22; 0,14; 0,10; 0,10; 0,09; 0,09 (курсивом выделены числа, которые суммируются при формировании списка 2).
Упорядоченный список 2 (5 чисел) 0,28; 0,26; 0,22; 0,14; 0,10
Упорядоченный список 3 (3 числа) 0,46; 0,28; 0,26;
3 Для последнего свернутого в п. 2 списка строится одноярусное кодовое дерево (из начальной вершины выходит 3 ребра, каждому из которых приписывается буква алфавита O, а каждой вершине 1–го яруса вероятности из последнего свернутого списка).
4 Строим 2–й, 3–й и другие ярусы кодового дерева, на которых разворачиваем просуммированные вероятности последнего, предпоследнего и т. списков(вершины, которым приписаны вероятности букв входного алфавита на любом ярусе, становятся концевыми); в результате таких действий получим кодовое дерево, в котором r концевых вершин и каждой из которых приписана вероятность pj. Выписав цепи из нулевой вершины к концевым (перечень ребер), получим схему кодирования с минимальной избыточностью.
Величина среднего превышения длины закодированного сообщения над длиной самого сообщения определим по формуле:
l* = = 0,26 + (0,28+0,46)х2 = 1,74.
Пример2: Построить код с минимальной избыточностью (код Хаффмана) для следующих исходных данных:
q =3; r = 7 в соответствии с формулой (12) m = 1. Для кодирования будет достаточно 1–го и 2–го ярусов обобщенного кодового дерева (см. рис.
r =(q m –n)+ q ×n – t, 7 = (3 –n)+ 3 n – t (подбираем целые n и t)
Равенство выполняется для n = 2 и t= 0.
Определим l* для полученной схемы по формуле (13)
l* = (( 3-2) х1 + (3х2 – 0) (1+1)) / 7 = 13/7 = 1,86.
Поможем в написании учебной работы
Поиск по сайту:Главная
О нас
Популярное
ТОП
Новые страницы
Случайная страница
Изречения для студентов
Пожаловаться на материал
Обратная связь
FAQ
Корректирующие коды Хемминга
Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока.
Поясним идею проверки на чётность на примере простейшего корректирующего кода, который так и называется, кодом с проверкой на чётность или кодом с проверкой по паритету (равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного кода добавляется один дополнительный разряд (символ проверки на чётность, называемый проверочным, или контрольным). Если число символов «1» в исходной кодовой комбинации чётное, то в дополнительном разряде формируют контрольный символ «0», а если число символов «1» нечётное, то в дополнительном разряде формируют символ «1». В результате общее число символов «1» в любой передаваемой кодовой комбинации всегда будет чётным.
Таким образом, правило формирования проверочного символа cводится к следующему:
r1 = i1 i2. ik,
Очевидно, что добавление дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению с числом комбинаций исходного первичного кода, а условие чётности разделяет все комбинации на разрешённые и неразрешённые. Код с проверкой на чётность позволяет обнаруживать одиночную ошибку при приёме кодовой комбинации, так как такая ошибка нарушает условие чётности, переводя разрешённую комбинацию в запрещённую.
Критерием правильности принятой комбинации является равенство нулю результата S суммирования по модулю 2 всех n символов кода, включая проверочный символ ri. При наличии одиночной ошибки S принимает значение 1:
S = r1 i1 i2. ik = 0 – ошибки нет;
S = r1 i1 i2. ik = 1 – однократная ошибка.
Этот код является (k + 1, k)-кодом, или (n, n – 1)-кодом. Минимальное расстояние кода равно двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с проверкой на чётность может использоваться только для обнаружения (но не исправления) однократных ошибок.
Увеличивая число дополнительных проверочных разрядов и формируя по определённым правилам проверочные символы r, равные 0 или 1, можно усилить корректирующие свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и основано построение кодов Хемминга. Рассмотрим эти коды, позволяющие исправлять одиночную ошибку, с помощью непосредственного описания. Для каждого числа проверочных символов r = 3, 4, 5. существует классический код Хемминга с маркировкой
(n, k) = (2r – 1, 2r – 1 – r), (4. 24)
– (7,4), (15,11), (31,26).
При других значениях числа информационных символов k получаются так называемые усечённые (укороченные) коды Хемминга. Так, для международного телеграфного кода МТК-2, имеющего 5 информационных символов, потребуется использование корректирующего кода (9,5), являющегося усечённым от классического кода Хемминга (15,11), так как число символов в этом коде уменьшается (укорачивается) на 6. Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и описать с помощью кодера, представленного на рис.
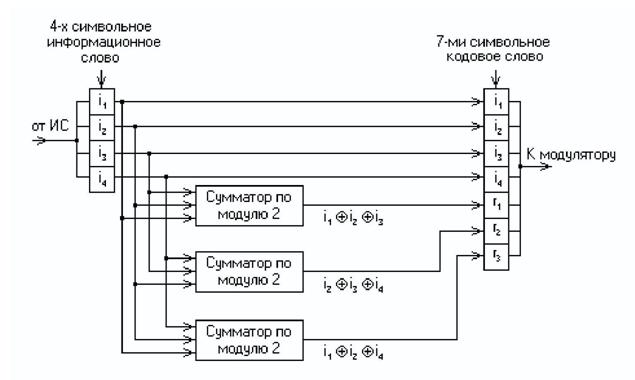
В простейшем варианте при заданных четырёх (k = 4) информационных символах (i1, i2, i3, i4) будем полагать, что они сгруппированы в начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы тремя проверочными символами (r = 3), задавая их следующими равенствами проверки на чётность, которые определяются соответствующими алгоритмами
r1 = i1 i2 i3;
r2 = i2 i3 i4;
r3 = i1 i2 i4,
На рис. 3 приведена схема декодера для (7,4)-кода Хемминга, на вход которого поступает кодовое слово:
V = (i′1, i′2, i′3, i′4 , r′1, r′2, r ′3).
Апостроф означает, что любой символ слова может быть искажён помехой в канале передачи.
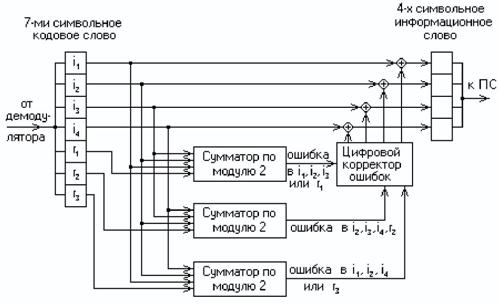
В декодере, в режиме исправления ошибок, строится последовательность:
s1 = r1’ i1’ i2’ i3’;
s2 = r2’ i2’ i3’ i4’;
s3 = r3’ i1’ i2’ i4’.
Трёхсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром» используется и в медицине, где он обозначает сочетание признаков, характерных для определённого заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой сочетание результатов проверки на чётность соответствующих символов кодовой группы и характеризует определённую конфигурацию ошибок (шумовой вектор).
Кодовые слова кода Хемминга для k = 4 и r = 3 приведены в табл.
Число возможных синдромов определяется выражением
S = 2r. 25)
При числе проверочных символов r = 3, имеется восемь возможных синдромов (23 = 8). Нулевой синдром (000) указывает на то, что ошибки при приёме отсутствуют или не обнаружены. Всякому ненулевому синдрому соответствует определённая конфигурация ошибок, которая и исправляется. Классические коды Хемминга (4. 20) имеют число синдромов, точно равное их необходимому числу, позволяют исправить все однократные ошибки в любом информативном и проверочном символах и включают один нулевой синдром. Такие коды называются плотноупакованными.
k = 4
r = 3
i1
i2
i3
i4
r1
r2
r3
Усечённые коды являются неплотноупакованными, так как число синдромов у них превышает необходимое. Так, в коде (9,5) при четырёх проверочных символах число синдромов будет равно 24 = 16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5).
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и соответствующие конфигурации ошибок.
Синдром
Конфигурация ошибок
Ошибка в символе
r3
r2
i4
r1
i1
i3
i2
Таким образом, код (7,4) позволяет исправить все одиночные ошибки. Простая проверка показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно создание такого цифрового корректора ошибок (дешифратора синдрома), который по соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе. После внесения исправления проверочные символы ri можно на выход декодера не выводить. Две или более ошибки превышают возможности корректирующего кода Хемминга, и декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и выдавать искажённые информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4) – кодами Хемминга.
Кодирование
Сначала в исходное сообщение добавляем контрольные биты и устанавливаем их в нуль. Контрольные биты располагаются в тех номерах битов, которые равны степеням двойки (ибо алфавит двоичный). То есть. Два в степени нуль — это единица, два в степени 1 = два, два в степени 2 = четыре, а два в степени 3 = восемь, два в степени 4 = 16
Значит контрольные биты будут находиться в «буквах»(битах) под номерами 1, 2, 4, 8 и 16.

В остальные номера бит переписываем исходное сообщение.

Видно, что длина «слова» из-за такой избыточности увеличилась на пять «букв». В данном случае, конечно. У вас количество дополнительных бит будет зависеть от длины исходного «слова».
Теперь нужно вычислить эти контрольные биты. Каждый контрольный бит с номером N «контролирует» непрерывную последовательность из N битов, через каждые N битов.
Вот на картинке отмечено иксами (X), какие биты нужно использовать для вычисления первого контрольного бита (с номером «1»)

Для вычисления контрольно бита нужно просто сложить все «буквы» нашего «слова», которые он контролирует, а затем принять нелёгкое решение: если сумма получилась чётная, то пишем в результате нуль, а если нечётная — единицу.
Вычисляем первый бит. Складываем биты под номерами 3,5,7,9,11,13,15,17,19,21
Это будет 0 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 = 5
Получилось 5 (пять). Сумма нечётная (на два нацело не делится). Значит пишем в первый бит единицу:

Теперь вычислим контрольный бит номер 2. Для него нужно будет найти сумму каждых двух бит следующих друг за другом непрерывно, через каждые два бита. Такие биты я тоже отметил на картинке.

То есть будем теперь суммировать биты, начитая с третьего по номеру, и далее те, которые отмечены иксом (X). Их номера 3, 6, 7, 10, 11, 14, 15, 18, 19. Это будет 0 + 0 + 0 + 1 + 0 + 0 + 1 + 1 + 1 = 4
Четыре — число чётное, значит оставляем в нашем втором бите нуль.

Переходим к вычислению третьего контрольного бита. Но это у нас он контрольный — третий. А в сообщении этот бит записан под номером 4 — четыре.

Значит и использовать будем все попадающие под наше правило биты, начиная с пятого. А это биты под номерами 5, 6, 7, 12, 13, 14, 15, 20, 21. Складываем их: 1 + 0 + 0 + 0 + 0 + 0 + 1 + 0 + 1 = 3
В итоге у нас нечётное число, значит пишем в наш контрольный бит единицу.

Осталось всего ничего — вычислить два оставшихся контрольных бита, которые под номерами 8 и 16.
В восьмом оставляем нуль потому, что в той последовательности, которую мы используем для вычисления присутствуют две единицы, дающие в сумме чётное число.

А в 16-м тоже сумма бит получается чётной — оставляем нуль:

В итоге мы получили слово с кодом Хэмминга, которое содержит избыточные биты (в сумме 21): «100110000100001011101».
Декодирование
А теперь представим, что к нам пришло сообщение с ошибкой. Вот оно «100110001100001011101». Мы знаем, что в него добавлены избыточные биты по алгоритму Хемминга, и нам надо проверить, есть в нём ошибка или нет.
Для этого нужно поступить следующим образом. Сначала вычисляем заново все контрольные биты по предыдущему алгоритму. Для этого сначала обнуляем все биты, находящиеся на номерах степеней двойки:

В первом оставляем нуль, ибо в подконтрольных битах чётное число единиц.

Вычисляем все остальные контрольные биты по описанному выше алгоритму (мне лень заново его описывать тут), и получаем, что не совпадают контрольные биты под номерами 1 и 8:

Теперь складываем номера этих контрольных бит: 1 + 8, и получаем 9 — номер бита, в котором закралась ошибка! Ура! Теперь просто меняем девятый бит на обратный — с единицы на нуль, — и получаем исходное сообщение!
Отметим, что это самый простейший алгоритм Хемминга, который может исправить только одну ошибку в слове. Об остальных алгоритмах данная статья умалчивает
