Принципы обнаружения и исправления ошибок в принятой кодовой комбинации циклического кода
Переданная кодовая комбинация двоичного циклического кода, представленная полиномом F(x), из-за искажений единичных элементов в каналах связи может быть принята с ошибками и иметь вид некоторого полинома Н(х). Если просуммировать по mod2 одноименные разряды F(х) и Н(х), то получим
где Е(х) – полином ошибок.
Разрядность полинома ошибок такая же, как и разрядность комбинации F(х) циклического кода. При этом ненулевые разряды в Е(х) указывают на ошибочные элементы в принятой кодовой комбинации Н(х). При отсутствии ошибок полином Е(х) состоит из одних нулей.
Принимая во внимание вышеприведенные обозначения, принятую кодовую комбинацию можно представить следующим образом:
Для обнаружения ошибок в принятой кодовой комбинации Н(х) следует разделить Н(х) на порождающий многочлен Р(х). Результат деления укажет на наличие или отсутствие ошибки в принятой кодовой комбинации Н(х). Если деление дает нулевой остаток, то ошибки отсутствуют или не обнаружены. Если же в результате деления полинома Н(х) на порождающий многочлен Р(х) остаток R’(х) отличен от нуля , то это означает что принятая кодовая комбинация Н(х) содержит ошибки (рис 2).
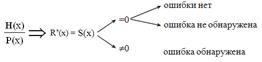
Рис.2. Схема выявления ошибок в принятой кодовой комбинации H(x)
Вид ненулевого остатка R’(x), называемого синдромом ошибки S(х), имеет однозначное соответствие с ошибочным разрядом и видом полинома однократной ошибки Е(х) для всех кодовых комбинаций Н(х) циклического кода. Например, для циклического кода (9,5) при заданном порождающем многочлене P(x)= x4 + x + 1 остаток R’(x) всегда будет иметь вид S(х)=0011, если ошибка возникла в пятом разряде входной кодовой комбинации, т.е. в младшем информационном разряде, независимо от вида переданной кодовой комбинации F(х).
Следует отметить, что остаток R’(x), получаемый при делении полинома Н(х), на порождающий многочлен Р(х), имеет такой же вид, как и остаток от деления Е(х) на Р(х), поскольку полином F(х) делится на Р(х) без остатка.
Кратность обнаруживаемых ошибок в принятой кодовой комбинации циклического кода определяется минимальным кодовым расстоянием dmin этого кода. Для циклического кода (9,5) значение dmin=3, что обеспечивает гарантированное обнаружение всех однократных и двукратных ошибок. Кроме того, код позволяет обнаруживать часть ошибок более высокой кратности, начиная с веса, равного dmin и более. Код не обнаруживает ошибки, если полином ошибки имеет вид разрешенной кодовой комбинации.
Номер такта, на котором в регистре-делителе возникает “особая” кодовая комбинация, указывает место ошибочного разряда в принятой кодовой комбинации Н(х). При считывании этой комбинации из буферного регистра ошибочный разряд должен быть исправлен (инвертирован).
Циклический код (9,5) гарантированно исправляет только однократные ошибки. Ошибки более высокой кратности код (9,5) не исправляет.
Заметим также, что деление полинома Н(х) на многочлен Р(х) и считывание информации из буферного регистра после 9го такта целесообразно осуществлять под действием “быстрых” тактовых импульсов. Это позволит без задержки принять из канала связи и обработать следующую кодовую комбинацию Н(х).
1. Структурная схема кодирующего и декодирующего устройства ( циклич. Коды ).

Образующий полином циклического кода
Основы передачи дискретных сообщений
Тема 5. Защита от ошибок в системах связи
От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность.
Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение.
Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов.
В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО.
5.1 Понятие о корректирующих кодах
Пусть имеется источник сообщений с объемом алфавита К.
, то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.
Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки.
Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия
, при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.
Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных.
Расстояние Хемминга – характеризует степень различия кодовых комбинаций и определяется числом несовпадающих в них разрядов.
Перебрав все возможные пары разрешенных комбинаций рассматриваемого кода можно найти минимальное расстояние Хемминга d0.
Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки.
У простого кода d0=1 – он не обнаруживает и не исправляет ошибки. Так как любая ошибка переводит одну разрешенную комбинацию в другую.
В общем случае справедливы следующие соотношения
– для обнаруживающей способности
– для исправляющей способности
Двоичный блочный код является линейным если сумма по модулю 2 двух кодовых слов является также кодовым словом.
Линейные коды также называют групповыми.
Введем понятия группы.
Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:
Если выполняется условие gi gj = gj gi, то группа называется коммутативной.
Поэтому используя свойство замкнутости относительно операции 2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.
Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.
В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.
5.2 ЦИКЛИЧЕСКИЕ КОДЫ
Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов:
если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.
Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.
Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Представление кодовой комбинации в виде многочлена.
Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов).
В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде
Запишем полиномы для конкретных 4-элементных комбинаций
Действия над многочленами.
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,
Рассмотрим операцию деления на следующем примере:
Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.
Отметим, что запись кодовой комбинации в виде многочлена, не всегда определяет длину кодовой комбинации. Например, при n = 5, многочлену
Алгоритм получения разрешенной кодовой комбинации циклического кода из комбинации простого кода
Пусть задан полином
, определяющий корректирующую способность кода и число проверочных разрядов r, а также исходная комбинация простого k-элементного кода в виде многочлена
Требуется определить разрешенную кодовую комбинацию циклического кода (n, k).
Формирование базиса (производящей матрицы) циклического кода
Формирование базиса циклического кода возможно как минимум двумя путями.
Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).
В данном случае код будет неразделимым.
Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом
Построение кодера циклического кода
Рассмотрим код (9,5) образованный полиномом
Разрешенная комбинация циклического кода
образуется из комбинации простого (исходного) кода путем умножения ее на
и прибавления остатка R(x) от деления
на образующий полином
Для реализации операции добавления нулей используется r-разрядный регистр задержки.
Это двоичное число и будет остатком
Построение формирователя остатка циклического кода
Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.
Сформулируем правила построения ФПГ.
Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.
4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.
Структурная схема кодера циклического кода (9,5)
Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.
Рассмотрим работу этой схемы
1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4
2. Во время пятого такта К2 – замыкается а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.
За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток
3. К2 – размыкается, К1 – замыкается и в след за информационными в линию уйдут элементы проверочной группы.
4. Одновременно идет заполнение регистров новой комбинацией.
Второй вариант построения кодера ЦК.
Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.
Устройство деления на производящий полином
За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).
За эти же 5 тактов информационные разряды, выданные сразу на модулятор.
Далее в след за информационными уходят проверочные из ячеек устройств деления.
Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.
Окончательно структурная схема экономичного кодера выглядит так.
— На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.
— После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;
— на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.
Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.
Определение ошибочного разряда в ЦК.
Пусть А(х)-многочлен соответствующий переданной кодовой комбинации.
Н(х)- многочлен соответствующей принятой кодовой комбинацией.
Тогда сложение данных многочленов по модулю два даст многочлен ошибки.
E(x)=A(x) H(x)
При однократной ошибке Е(х) будет содержать только один единственный член соответствующий ошибочному разряду.
Остаток – полученный от деления принятого многочлена H(x) на производящей Pr(x) равен остатку полученному при делении соответствующего многочлена ошибок E(x) на Pr(x)
При этом ошибке в каждом разряде будет соответствовать свой остаток R(x) (он же синдром), а значит, получив синдром можно однозначно определить место ошибочного разряда.
Алгоритм определения ошибки.
Пусть имеем n-элементные комбинации (n = k + r) тогда:
2. Делим полученный полином Н(х) на Pr(x) и получаем текущий остаток R(x).
3. Сравниваем R0(x) и R(x).
— Если они равны, то ошибка произошла в старшем разряде.
— Если «нет», то увеличиваем степень принятого полинома на Х и снова проводим деления
в) Опять сравниваем полученный остаток с R0(x)
— Если они равны, то ошибки во втором разряде.
— Если нет, то умножаем Н(х)х 2 и повторяем эти операции до тех пор, пока R(X) не будет равен R0(x).
Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.
то номер ошибочного разряда 3+1=4
Пример декодирования комбинации ЦК.
Положим, получена комбинация H(х)=111011010
Проанализируем её в соответствии с вышеприведенным алгоритмом.
Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х 8 на производяший полином P(x)=X 4 +X+1
X 8 +X 5 +X 4 x 4 +x+1
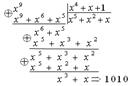
Разделим принятую комбинацию на образующий полином
Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.
Декодер циклического кода с исправлением ошибки
Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ.
На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.
Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.
В нашем случае инвертируется второй разряд на 11 такте.
5.3 Выбор образующего полинома
Рассмотрим вопрос выбора образующего полинома, который определяет корректирующие свойства циклического кода. В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов mi(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома x n + 1:
Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов:
для любых значений l и tи.ош существует циклический код длины n =2 l – 1, исправляющий все ошибки кратности tи.ош и менее, и содержащий не более
После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:
Таблица минимальных многочленов
Вид минимальных многочленов для
Определяя образующий полином, нужно из столбца для соответствующего соотношения
выписать все многочлены, начиная с верхней строки до нижней с номером j=2tи.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (*). В частности, если r=3, tи.ош=1, j=2*1-1=1, образующий полином будет представлять собой единственный минимальный многочлен P(x)= m1(x) = x 3 +x+1 (первая строка, второй столбец таблицы ). Соответственно образующее число равно 1011.
Алгоритм декодирования
Для кодового слова синдром, как известно, равен 0. В данном случае это не так, посланное слово было искажено помехой. В соответствии с описанной процедурой декодирования будем вычислять s i (x) = x i (x 2 + x 6 + x 8 )(mod g(x)) для последовательных возрастающих значений i пока не найдем многочлен степени меньшей или равной двум (число ошибок t = 2 ).
s 1 = xs(x)(mod g(x)) = (x 3 + x 7 + x 9 )(mod g(x)) = x 3 + x 4 + x 5 + x 6 + x 7
s 2 = x 2 s(x)(mod g(x)) = (x 4 + x 8 + x 10 )(mod g(x)) = 1 + x + x 2 + x 5
s 3 = x 3 s(x)(mod g(x)) = (x 5 + x 9 + x 11 )(mod g(x)) = x + x 2 + x 3 + x 6
s 4 = x 4 s(x)(mod g(x)) = (x 6 + x 10 + x 12 )(mod g(x)) = x 2 + x 3 + x 4 + x 7
s 5 = x 5 s(x)(mod g(x)) = (x 7 + x 11 + x 13 )(mod g(x)) = 1 + x 3 + x 5 + x 6 + x 7
s 6 = x 6 s(x)(mod g(x)) = (x 8 + x 12 + x 14 )(mod g(x)) = x + 1
Итак, если отправленное кодовое слово имеет не более двух ошибок, то оно было таким
(x + x 2 + x 4 + x 6 + x 7 + x 8 + x 10 + x 13 ) + (x 10 + x 9 ) =
x + x 2 + x 4 + x 6 + x 7 + x 8 + x 9 + x 13
Размерность, порождающая и проверочная матрицы
c 1 (x) c 2 (x) = a 1 (x)g(x)a 2 (x)h(x) = a 1 (x)a 2 (x)f(x) = 0 (mod f(x)),
Рассмотрим два вектора:
и их произведение (вернее, соответствующих многочленов)
для каких-то c i из F. Свободный член произведения
т.к x n = 1 (mod f(x)). Теперь c 0 можно записать как скалярное произведение
где b’ теперь вектор, связанный с x n-t b(x). По отношению к b(x), b’ это вектор, полученный циклическим сдвигом b на t+1 позиций влево с последующим изменением порядка координат на противоположный.
Коэффициент при x 2 будет a (b 2 b 1 b 0 ). Этот вектор b’ получен из b сдвигом на 3 ( = 2 + 1) позиции влево (это ставит все координаты на старые места) и изменением порядка координат с последней на первую. b-вектор в коэффициенте при x получается из b сдвигом на 2 ( = 1 + 1) позиции влево, что дает (b 2 b 0 b 1 ) и изменением порядка следования (b 1 b 0 b 2 ).
Порождающая матрица для C’
Перепишем колонки G’ в обратном порядке, получим порождающую матрицу для C perp (она же проверочная для исходного кода)
Заметим, что h R (x) = x k h(1/x), где k = deg h(x). Суммируя все вышесказанное, получим следующее.
Синдромы и охота на ошибки
где deg(r i (x)) i (x) = 0. Then
система k линейно независящих кодовых слов, матрица, по строкам которой записаны эти слова, есть порождающая матрица требуемого вида.
x 3 = (1)(x 3 + x + 1) + (1+ x)x 4 = (x)(x 3 + x + 1) + (x + x 2 )x 5 = (x 2 + 1)(x 3 + x + 1) + (1 + x + x 2 )x 6 = (x 3 + x + 1)(x 3 + x + 1) + (1 + x 2 ).
Порождающая матрицаЗаметим, что строки R как раз остатки от деления.
Если разделить r(x) на g(x), то получим
r(x) = (x 3 + 1)g(x) + (x + x 2 ),
Пример : g(x) = 1 + x 4 + x 6 + x 7 + x 8 порождает бинарный (15,7)-циклический код. Если минимальное расстояние 5(так), то t = 2. Некоторые (по меньшей мере) веса 2 маски ошибок могут содержать сдвиги не менее 7 0й и могут бытьотловлены. Если мы получили
r = (1100 1110 1100 010)
r(x) = (x + x 2 + x 4 + x 5 )g(x) + (1 + x 2 + x 5 + x 7 ).
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Коды Хемминга
В отличие от канонического матричного кода, в коде Хемминга информационные и проверочные биты не разнесены в отдельные подматрицы, а чередуются. Если биты кодовой комбинации пронумеровать, начиная с 1, слева направо, то контрольными (проверочными) оказываются биты с номерами 1, 2, 4, 8 и т.д., все остальные являются информационными. Цель этих перестановок — сделать так, чтобы синдром ошибки непосредственно указывал на локализацию ошибок, минуя промежуточную таблицу соответствия синдромов и ошибок или исключая необходимость сравнения синдрома ошибки со столбцами проверочной матрицы. Код Хемминга начинают строить с проверочной матрицы Я, так как ее вид очевиден: столбцы проверочной матрицы представляют собой набор синдромов, соответствующих двоичному представлению номера столбца. Затем строят порождающую матрицу G, исходя из того, что матрицы Я и G ортогональны, т.е. скалярное произведение каждой строки матрицы G на каждую строку матрицы Я равно нулю, т.е.

Построим код Хемминга для (7,4)-кода. Чтобы синдром ошибки указывал на место ошибки, проверочная матрица должна иметь вид:

Обратите внимание, каждый столбец матрицы Н является двоичным представлением номера этого столбца.
В матрице Н на первом, втором и четвертом местах стоят столбцы матрицы, имеющей единицы на второстепенной диагонали, а на остальных — столбцы, соответствующие информационным разрядам кода. Выделим подматрицу, соответствующую информационным разрядам (т.е. третий, пятый, шестой и седьмой столбцы):

Повернем матрицу Н, по часовой стрелке и получим проверочную подматрицу порождающей матрицы:

Поставим столбцы матрицы Р на первое, второе и четвертое места, а остальные столбцы будут столбцами единичной матрицы. Получим порождающую матрицу кода Хемминга:


Проверим разрешенное кодовое слово, вычислив синдром:

Синдром нулевой, следовательно, получена разрешенная кодовая комбинация.

Синдром представляет собой двоичное число 3, что локализует ошибку в третьем разряде.
8 Построить блочный систематический код для исправления двукратных ошибок Решение:
Порождающая матрица (8, 3)-кода уже была получена:

Представим ее в каноническом виде, переставив столбцы:

Выделим проверочную подматрицу:


Составим проверочную матрицу (8, 3)-кода:

8 Как можно использовать полученный код для решения задачи о разведчиках?
Командир должен пронумеровать своих бойцов от 1 до 8. В соответствии с порождающей матрицей G бойцы с номерами 1,4, 5 должны отправиться по 1-й дороге, номера 2,6, 7 — по второй дороге, а разведчики с номерами 3 и 8 — по третьей дороге. Проверка результатов разведки может осуществляться следующим образом.
Первый случай. Допустим, объект находится на первой дороге, а шпионами являются бойцы № 1 и 5. Обнаружив объект, они солгут, и командир получит следующее сообщение: 0= (00010000). Умножив сообщение на проверочную матрицу, командир получит ненулевой синдром и обнаружит ложь:

Второй случай. Допустим, что объект находится на 1-й дороге, а шпионы — это бойцы № 2 и 8. С учетом искажений во 2-м и 8-м разрядах, командир получит следующее сообщение: U = (11011001). Проверка вновь осуществляется перемножением проверочной матрицы на сообщение:

Ненулевой синдром свидетельствует об ошибке.
Третий случай. Объект находится на 1-й дороге и в докладе разведгрупп нет искажений (шпионы воздержались от лжи). Тогда сообщение будет выглядеть так: 0 = (10011000). Умножение проверочной матрицы на эту кодовую комбинацию даст нулевой синдром, свидетельствующий об отсутствии искажений.
8 Можно ли не только обнаружить объект, но и установить, кто из бойцов является шпионами?
Однако заметим, что если наряду с двукратными ошибками учитывать однократные (т.е. один из шпионов солжет, а второй скажет правду), то всего возможны 28 + 8 = 36 различных ошибок. Это превышает количество возможных синдромов и, следовательно, не все такие ошибки могут быть локализованы.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали
, а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину
, равную количеству различающихся цифр в соответствующих разрядах цепочек
, так как все цифры в соответствующих позициях равны, а вот
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Полиномиальная арифметика
Для тех, кто это подзабыл, приведем пример на деление.
Пример 1
Напомним также модульную арифметику многочленов. Многочлены называются сравнимыми по модулю многочлена p(x), если их разность делится на p(x) нацело. Поэтому для получения f(x)(mod p(x)) вам нужно просто разделить f(x) на p(x) и взять остаток от деления. Заметим, что если степень f(x) меньше степени p(x), то результатом будет просто f(x)
Пример 2
Замечательным свойством полиномиального представления кодов является возможность осуществить циклический сдвиг на одну позицию вправо простым умножением кодового многочлена степени n-1 на многочлен «x» и нахождения остатка от деления на x n + 1.
Пример 3
Циклические коды позволяют обнаруживать и исправлять групповые ошибки. В циклических кодах широко используется операция циклической перестановки (самый старший разряд переставляется в конец кодовой комбинации, а остальные сдвигаются влево или, наоборот, младший разряд переставляется в начало, остальные сдвигаются вправо).
При формировании циклических кодов происходит деление на образующий полином.
Представление кодовой комбинации в виде полинома.
Q(x)=111111=x 5 +x 4 +x 3 +x 2 +x 1 +x 0
xi – двоичный разряд. x 1 =x, x 0 =1
Если какой-либо разряд xi = 0 в составе полинома, то его опускают.
Q(x)=1100110=x 6 +x 5 +x 2 +x
Образующий полином – это полином, который является простым числом: (11)10, (13)10, (17)10, (19)10 и т.д. Он выбирается заранее как делитель, позволяющий выполнять обнаружение и исправление ошибки.
P(x)=(11)10=(1011)2=x 3 +x+1 Степень образующего полинома – к. (к=3)
Операция деления полинома на полином.
Деление сходно с алгебраическим, но есть отличие:
деление заканчивается, если наивысшая степень у остатка меньшей таковой у делителя;
интерес представляет не частное от деления, а остаток.
Рассмотрим пример деления.




5 + x 3 + x 2
Остаток: R (x) = x 2 + x = 110
Формирование циклического кода.
Величина k показывает количество сдвигов влево, которое Q(x) должно претерпеть.
Пример: Q(x) = x 5 + x 3 + x = 101010 – исходная КК,
110 – контрольная часть
Остаток R(x) называется синдромом..
Пусть Q(x) = 1110. Если k =3, то Q(x) X k = 1110 000
Проверка правильности циклического кода.
В алгоритме используются циклические сдвиги влево и вправо, количество которых подсчитывается во время выполнения.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
В матричном виде эта система будет иметь вид
Транспонирование здесь нужно потому, что
Будем называть матрицу
проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение
, мы получим один из кодов, который принадлежит окрестности
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Выбор образующего полинома
При построении циклических, кодов ответственным этапом является выбор образующего (порождающего) полинома.
Правила выбора полинома зависят от требуемой корректирующей способности кода, при этом образующий полином должен обеспечивать как можно большее количество остатков при делении на кодовые комбинации. Выработаны и предлагаются следующие общие правила выбора образующего полинома при построении любого циклического кода:
1.Степень образующего полинома должна быть не меньше числа проверочных символов r
2. Любой многочлен g(х) степени (n-к), который делит без остатка двучлен X n +1 может быть порождающим многочленом (n, к) циклического кода.
3. Образующий полином должен быть как можно более коротким.
4. Число ненулевых членов образующею полинома должно быть не меньше dмин.
Поскольку в циклическом коде опознавателями ошибок являются остатки от деления, то Р(х) должен обеспечивать требуемое число разлитых остатков. Обнаруживающая способность циклического кода определяется не только степенью обнаруживающего полинома. но и числом его членов.
Чем больше остатков может быть образованно при делении кодовой комбинации на образующий полином, тем выше корректирующая способность кода.
Образующий полином Р(х) циклического кода должен быть примитивным, т.е. входить в качестве сомножителя в разложение
Не всякий многочлен степени r, входящий в разложение данного двучлена, может быть использован для образования нужного (n, k)-кода.
Чтобы выяснить, какое из произведений может быть использовано в качестве образующего полинома, необходимо для каждого из них построить так называемую дополнительную матрицу. Эта матрица строится путем деления циклических сдвигов единицы с приписанными справа нулями на соответствующее произведение полиномов. При построении дополнительной матрицы Сr,k. по выбранному полиному необходимо также учитывать количество строк в цикле чередования проверочных разрядов и вес каждой строки (количество единиц).
Боуз и Чоудхурн показали, что для любых, целых положительных чисел m и tи существует циклический код элементности
с кодовым расстоянием
При этом число проверочных символов r не превышает величины mtu т.е.
r 2^ m +1= x n +1=x 15 +1.
Чтобы выяснить, какой из трех полиномов восьмой степени может быть использован в качестве образующего, найдем для каждого из них дополнительную матрицу С8.7— (к=15-8=7). Делением единицы с приписанными справа нулями и ее циклических сдвигов на 111010001 10001011 и 110111011 находим соответственные дополнительные матрицы

Так как каждая строка единичной матрицы Е- имеет вес равный единице, вес любой строки дополнительной матрицы должен быть не менее четырех единиц. Это требование, будет выполнено, если в качестве образующего полинома для построения циклического (15, 7)-кода выбрать одно из двух произведений: Р1(х 4 )Рз(х 4 ) или Р2(х 4 )Рз(х 4 )=
В третьей дополнительной матрице С8.7 из семи строк третья, четвертая и пятая не обладают требуемым весом. Поэтому произведение Р1(х 4 )Р2(х 4 ) не может быть использовано в качестве образующего полинома для построения циклического (.15, 7)-кода.
Коды Хэмминга
Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H(n,k), имеющей
столбцов, причем столбцами H(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до
Длина кодовой комбинации кода Хэмминга равна
Число информационных элементов определяется как
Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.
Зная вид матрицы H(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбца H(n,k) не являются линейно зависимыми. Наряду с этим, для любого числа m всегда можно указать три столбца матрицы H(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэмминга dmin=3.
Код Хэмминга является одним из немногочисленных примеров совершенного кода.
Действительно, поскольку (n, k) – код Хэмминга исправляет все одиночные ошибки, то все образцы одиночных ошибок (а их всего насчитывается
вариантов) должны разместиться в различных смежных классах, число которых также равно
При фиксированном числе
можно построить код Хэмминга любой длины (
) путем укорочения (n, k) – кода. Укорочение не уменьшает минимальное кодовое расстояние. В силу того, что для любого числа n существует код Хэмминга, любой групповой код с исправлением одиночных ошибок принято называть кодом Хэмминга.
Пример 5.13. Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.
Очевидно, что минимальная длина кода Хэмминга, имеющего практическое значение, есть 3. При увеличении n отношение
Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:
Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3( к примеру 1, 2 и 3), следовательно, dmin=3.
В том случае, когда столбцы матрицы H(n,k) – кода Хэмминга есть упорядоченная запись m – разрядных двоичных чисел, декодирование осуществляется оригинальным образом. В результате вычисления проверочного соотношения для кодовой комбинации
, имеющей одиночную ошибку, получается синдром
Пример 5.15. Пусть приемник УЗО системы передачи данных зарегистрировал комбинацию
т.е. ошибка в четвертом элементе и кодовая комбинация кода (7,4), которая была передана, имеет вид:
Путем несложных преобразований из (n, k) – кода Хэмминга с dmin=3 можно получить (n+1, k) – код Хэмминга с dmin=4.
Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.
Матрица проверок для (n+1, k) – кода Хэмминга с dmin=4 получается из матрицы проверок (n, k) – кода с dmin=3 путем введения дополнительной строки из (n+1)-ой единицы.
Так как размерность матрицы проверок кода с dmin=4 должна быть равна
, то к каждой строке матрицы проверок кода с dmin=3, необходимо добавить один нулевой элемент для того, чтобы не нарушить введенные ранее проверки. Матрица проверок для (n+1, k) – кода dmin=4 имеет вид:
Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.
Пример 5.16. Построить код Хэмминга (8,4) с dmin=4 на основе матрицы проверок кода (7,4).
По виду матрицы
можно сделать вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на четность.
Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.
Таким образом, матрице
Для того, чтобы получить код (8,4) с dmin=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:
Определим известным способом dmin (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) dmin=4.
Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).
Зная места проверочных элементов, легко привести матрицу H(n,k) кода Хэмминга к канонической форме.
Пример 5.18. Преобразовать матрицу
Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:
Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.
Оценим эффективность кодов Хэмминга.
Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратности S=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:
Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:
Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:
Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:
На основе (n, n-1) – кодов с dmin=2 или кодов Хэмминга с dmin=3 и dmin=4 можно построить коды с более высокими корректирующими свойствами. Для этой цели, наряду с защитой каждой передаваемой комбинации описанным выше способом, осуществляют помехоустойчивое кодирование одноименных разрядов групп передаваемых комбинаций. Процесс кодирования можно пояснить при помощи рис. 5.6.
Комбинации простого кода, подлежащие передаче по системе связи, записываются в виде таблицы – каждая комбинация составляет отдельную строку этой таблицы (информационные символы). Затем осуществляется кодирование по строкам и столбцам. В общем случае для кодирования строк и кодирования столбцов можно использовать различные коды. Избыточные элементы дописываются к каждой строке (проверка по строкам) и к каждому столбцу (проверка по столбцам). Проверка проверок осуществляется кодированием столбцов, составленных из избыточных элементов строк или кодированием строк, составленных из проверок столбцов. Последующее введение избыточности осуществляется для защиты блоков информации, представленных на рис. 5.6. Процесс кодирования поясняется на рис. 5.7. Из блоков информации, защищенных двумя проверками, составляется параллелепипед. Избыточные разряды третьей проверки образуют параллелепипед, выделенный утолщенной линией.
В результате итеративного кодирования получаются групповые коды, которые обладают следующим важным свойством.
Теорема 5.3. Минимальное кодовое расстояние итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.
Действительно, если в случае двух проверок минимальный вес одного кода равен
, а другого
, то вектор итеративного кода имеет, по крайней мере,
единиц в каждой строке и
элементов в каждом столбце и, следовательно, не менее
Аналогичные рассуждения можно продолжить и на случай большего числа проверок.
Порождающая матрица итеративного кода может быть построена следующим образом.
Пусть GA – порождающая матрица кода, используемого для проверки по строкам, а GВ – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (GAВ) имеет вид:
означает, что на местах “1” в матрице GA записывается матрица GВ, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам GВ. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то
Поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов
с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив
к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Порождающий многочлен
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами
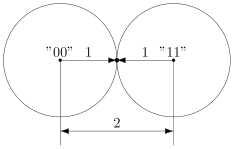
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
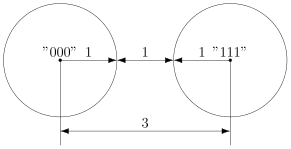
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием
будет успешно работать в канале с
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает
ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
, откуда получаем, что такой код может исправить до
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы
варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Наиболее распространенным систематическим линейным блочным кодом является код Хэмминга. К нему относятся коды с минимальным кодовым расстоянием dmin=3, способные исправлять однократные ошибки.
При передаче кодового слова по каналу связи возможно возникновение однократной ошибки в любом из его элементов. Количество таких ситуаций

. Таким образом, для того чтобы определить место возникновения ошибки, количество комбинаций проверочных элементов 2r должно быть не меньше количества возможных ошибочных ситуаций в коде плюс ситуация, когда ошибка не возникает, т. е. должно выполняться неравенство
Из этого неравенства следует минимальное соотношение проверочных и информационных разрядов, необходимое для исправления однократных ошибок
Для расчёта основных параметров кода Хэмминга можно задать количество проверочных элементов r, тогда длина кодовых слов n ≤ 2 r -1, а количество информационных элементов k=n—r. Соотношения между r, n и k приведены в следующей таблице (табл. 3.3.)
Характерной особенностью проверочной матрицы кода с dmin=3 является то, что ее столбцы – различные ненулевые комбинации длины r.
Например, для r=3 проверочная матрица кода Хэмминга имеет вид
Проверочная матрица (k, n)-кода Хэмминга составляется из n=2 r -1 строк и r столбцов и представляет собой двоичные комбинации числа i, где i – номер столбца проверочной матрицы (разряда кодовой комбинации).
Синдром, определяющий систему проверочных уравнений кода, находится из уравнения u
Например, для r=3 система проверочных уравнений будет следующей:
Отсюда проверочные разряды (контрольные суммы) находятся как
^ Чтобы закодировать сообщение m, в качестве u i, где i не равно степени 2, берутся соответствующие биты сообщения, а проверочные разряды с индексами степени 2 находятся из системы проверочных уравнений кода. В каждое уравнение системы входит только одна контрольная сумма.
Пример 1 Закодируем сообщение m=(0 1 1 1) (4, 7)-кодом Хэмминга.
Из системы проверочных уравнений находим контрольные суммы:
Таким образом, кодовым словом будет последовательность (0001111).
Пример 2 Сообщение кодируется (4, 7)-кодом Хэмминга. Принята последовательность y=(0011111). Декодируем принятый вектор.
Определяем синдром принятого вектора:
т. е. ошибка произошла в третьем разряде.
Исправляем ошибку, изменяя значение в третьем бите
Переданное сообщение декодируется как
Порождающей матрицей (k, n)-кода Хэмминга является матрица (k×n), в которой столбцы с номерами не степенями 2 образуют единичную подматрицу, а остальные столбцы соответствуют проверочным уравнениям кода. Такая матрица при кодировании будет копировать биты сообщения в позиции, не степени 2, и заполнять другие позиции кода согласно системе вычисления контрольных разрядов.
Пример 3 Система проверочных уравнений (4, 7)-кода Хэмминга следующая:
Соответственно порождающая матрица данного кода имеет вид
Список использованной и рекомендуемой литературы
Вид ненулевого остатка R’(x), называемого синдромом ошибки S(х), имеет однозначное соответствие с ошибочным разрядом и видом полинома однократной ошибки Е(х) для всех кодовых комбинаций Н(х) циклического кода. Например, для циклического кода (9,5) при заданном порождающем многочлене P(x)= x 4 + x + 1 остаток R’(x) всегда будет иметь вид S(х)=0011, если ошибка возникла в пятом разряде входной кодовой комбинации, т.е. в младшем информационном разряде, независимо от вида переданной кодовой комбинации F(х).
Заметим также, что деление полинома Н(х) на многочлен Р(х) и считывание информации из буферного регистра после 9 го такта целесообразно осуществлять под действием “быстрых” тактовых импульсов. Это позволит без задержки принять из канала связи и обработать следующую кодовую комбинацию Н(х).
1. Структурная схема кодирующего и декодирующего устройства ( циклич. Коды ).
