Раздел разработан в 2010 г. при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом КОДИРОВАНИЕ
.
В информатике и телекоммуникациях, коды Хэмминга являются семейством линейного исправления ошибок коды. Коды Хэмминга могут обнаруживать до двух битовых ошибок или исправлять однобитовые ошибки без обнаружения неисправленных ошибок. Напротив, простой код четности не может исправлять ошибки и может обнаруживать только нечетное количество битов с ошибкой. Коды Хэмминга – это совершенные коды, то есть они достигают наивысшей возможной скорости для кодов с их длиной блока и минимальным расстоянием, равным трем. Ричард В. Хэмминг изобрел коды Хэмминга в 1950 году как способ автоматического исправления ошибок, вносимых считывающими устройствами перфокарт. В своей оригинальной статье Хэмминг развил свою общую идею, но специально сосредоточился на коде Хэмминга (7,4), который добавляет три бита четности к четырем битам данных.
В математические термины, коды Хэмминга – это класс двоичных линейных кодов. Для каждого целого числа r ≥ 2 существует код с длиной блока n = 2 – 1 и длиной сообщения k = 2 – r – 1. Следовательно, скорость кодов Хэмминга равна R = k / n = 1 – r / (2 – 1), что является максимально возможным для кодов с минимальным расстоянием, равным трем (т. е. минимальное количество битовых изменений, необходимых для перехода от любого кодового слова к любому другому кодовому слову, равно трем) и длина блока 2-1. Матрица проверки на четность кода Хэмминга строится путем перечисления всех столбцов длины r, которые не равны нулю, что означает, что двойной код из код Хэмминга – это сокращенный код Адамара. Матрица проверки на четность имеет свойство, состоящее в том, что любые два столбца являются попарно линейно независимыми.
Из-за ограниченной избыточности, которую коды Хэмминга добавляют к данным, они могут обнаруживать и исправлять ошибки только при низком уровне ошибок. Это случай компьютерной памяти (ECC-память ), где битовые ошибки крайне редки, а коды Хэмминга широко используются. В этом контексте часто используется расширенный код Хэмминга, имеющий один дополнительный бит четности. Расширенные коды Хэмминга достигают расстояния Хэмминга, равного четырем, что позволяет декодеру различать, когда возникает не более одной однобитовой ошибки, и когда возникают любые двухбитовые ошибки. В этом смысле расширенные коды Хэмминга предназначены для исправления одиночной ошибки и обнаружения двойной ошибки, сокращенно SECDED .
На прошлом занятии мы разобрали проблему кодирования и увидели, что закодированный сигнал можно получить с помощью матрицы генератора. Мы разобрали пример этой матрицы для кода Хемминга (7, 4).
Пример был такой: на вход подавалась последовательность бит 1010 (назовём её K), далее она пропускалась через классический кодер, умножалась на матрицу генератора — G (как это делается смотрите в прошлой лекции). На выходе мы получили закодированное слово
длиной 7 бит: 4 бита данных и 3 контрольных.
Далее эта посылка отправляется по каналу связи, в котором действуют шумы, помехи, и должна добраться до приемника.
Приемник регистрирует этот сигнал на какую-то антенну. Далее этот сигнал оцифровывается и отправляется на вход декодера, который должен из данной посылки вытащить наши информационные биты.
Представим наш кодер, далее сигнал подводится к передатчику и к антенне, которая излучает сигнал, в котором есть какие-то помехи, наводки. Сигнал проходит через этот канал связи, испытав на себе «прелести» шумов, поступает на приемную антенну. С приемной
антенны через аналогово-цифровой преобразователь поступает в декодер.
Визуализируем наш сигнал: 1011010
За счёт всплеска шумов в конце приёмник примет сигнал 1011011. То есть аналого-цифровой преобразователь (АЦП) понял, что на конце сообщения был сигнал, поэтому в этот бит записал 1, что, конечно же, является ошибкой.
Теперь посмотрим, как декодер может справиться с этой задачей. Фактически декодер должен решить обратную задачу относительно кодера. На вход декодера поступает n символов, он должен проверить есть ли ошибки, и если есть, то исправить их, и затем
удалить контрольные биты — k. По аналогии с матрицей, которая кодирует, есть проверочная матрица, обозначается как H, она выглядит очень похоже на матрицу генератора, но отличается. Для кода Хэмминга (7, 4), который сейчас рассматриваем, эта
проверочная матрица выглядит следующим образом:
Обратите внимание на блок из четырёх последних столбцов матрицы H, фактически он соответствует блоку из первых трёх столбцов генераторной матрицы G, который повёрнут на 90 градусов:
То есть можно написать проверочную
матрицу H на основе генераторной (G).
Теперь попробуем умножить проверочную матрицу H на тот код, который получили, обозначим его CwR, где R — от слова “receive” принятый. Умножение производится по правилу: строка первой матрицы умножается посимвольно на
столбец второй, после чего значения записываются в столбик и суммируются по модулю 2:
В результате сложения всех значений в каждой строке получается 3, по основанию 2 это равно единице, соответственно получаем матрицу из одного столбца и трёх строк, в каждой из которых стоит единица. Эта матрица называется
синдромом.
Мы получили ненулевой синдром, следовательно в сообщение закралась ошибка.
А теперь в проверочной матрице H найдём столбец, который равен синдрому — это седьмой столбец. следовательно ошибка в седьмом бите!
Далее исправляем ошибку в сообщении 1011011 (ошибка в седьмом символе), следовательно правильное сообщение будет с противоположным значением в этом символе, то есть равно 0, а не 1, и итоговое исправленное сообщение будет 1011010.
Если теперь проверочную матрицу умножить на исправленное сообщение, то синдром будет равен нулю, а это значит, что ошибок нет. Если нет ошибок, то декодер знает, что последние четыре символа сообщения — это данные, а первые три — контрольные символы,
и он оставляет только данные, а контрольные удалит.
Как видите, чтобы закодировать слово,
нужно исходное слово наложить на
матрицу-генератор, а там используется только сложение и умножение. Чтобы
декодировать сообщение, нужно проверочную
матрицу умножить на принятый сигнал,
определить синдром, если он ненулевой,
то по его виду найти ошибку и исправить, и тут тоже используется сложение и умножение по модулю 2, а это очень быстрая операция, поэтому кодер и декодер работают достаточно быстро.
Мы рассмотрели как устроены генерирующая матрица и проверочная на примере кода Хэмминга (7, 4), но подобные матрицы могут быть сгенерированы для любых блочных кодов, например для кода Хэмминга (15, 11), где 11 информационных и 4 проверочных, то есть в
сумме блок состоит из 15 бит, и так далее.
Вообще говоря, так как коды Хэмминга исправляют однократную ошибку, а для того чтобы передать сигналы на далёкое расстояние, мы помним, что амплитуда сигнала падает с расстоянием, и поэтому шумы сильнее начинают влиять на сигнал, то могут возникнуть и
неоднократные ошибки, но и больших кратностей. Для того чтобы избежать такие ошибки используют более сложные коды, например,
код Голея. Он использовался для передачи данных с бортов Вояджер 1 и Вояджер 2, когда они пролетали с Юпитером и Сатурном. И там использовался код (23, 12), то есть 12 информационных бит, позволял исправлять трёхкратную ошибку, что существенно повышает
надёжность кода.
На рисунке 4 вы можете увидеть матрицу-генератор для кода Голея (23, 12).
На рисунке 5 вы можете увидеть матрицу-генератор для расширенного кода Голея (24, 12). Сейчас он используется чаще, так как кратен восьми (24 бита — это 3 байта), и удобнее с ним работать.
А на рисунке 6 изображена проверочная матрица для кода Голея (24, 12), где чёрные кружочки соответствуют 1, а белые — 0.
В вашей работе, используя тот же аппарат, который рассмотрели для кода Хэмминга, вы можете использовать и для кода Голея, воспользовавшись этими матрицами. Попробуйте закодировать сигнал самостоятельно.
Так как код длины 12, то можно сгенерировать 4096 различных вариантов сообщений. А вариантов сообщений, которые можно получить, 224 — достаточно большой объём данных. Таблицу на 224 сейчас можно построить, так как
существующие современные средства и компьютеры позволяют методом грубой силы определять нужный код. Есть конечно алгоритмы более умные, которые позволяют решать эту задачу быстрее, чем прямым перебором.
Следующее продвижение, связанное с помехоустойчивыми кодами, — это использование кодов Рида–Соломона, которые уже используют не бинарный алфавит (0 и 1), а на основе более богатых алфавитов. Эти коды являются блочным — кодируют
отдельный блок целиком — но для того, чтобы разобраться как они работают, придётся достаточно глубоко копнуть в алгебру, то есть там достаточно алгебраический подход, когда создаётся некоторый генерирующий полином, который позволяет сформировать
закодированное слово и соответственно декодировать.
Эти коды обладают большей
помехоустойчивостью, поскольку позволяют
избавляться от многократных ошибок при
относительно небольшой избыточности
кодов. С ними можно будет познакомиться, когда вы поступите на первый–второй курс института и разберётесь с темой алгебраического подхода для генерации помехоустойчивого кода более подробно.
А вообще говоря, коды Рида–Соломона часто используются, когда записывается, например, на лазерный диск какая-то информация. Если посмотреть на многократно использованный диск, то можно легко увидеть множество царапин, иногда трещин, но тем не менее данные
с него читаются. Это говорит о высокой надёжности этого кода, но и избыточность у него около 40%, и при этом он используется довольно часто. Разработчики программного обеспечения на Вояджерах сумели на лету перепрограммировать Вояджеры,
и они передавали данные, используя код Рида–Соломона.
Для размышления
Пусть в рассмотренном сегодня примере при передаче сигнала 1011010 изменился не последний бит, а четвёртый, то есть принято было сообщение 1010010. Используя продемонстрированный подход, попробуйте её обнаружить.
Материалы
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
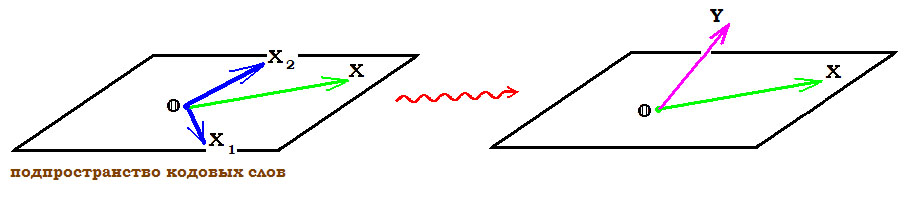
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
Вывод. Для однозначного обнаружения места ошибки7) достаточно, чтобы все столбцы матрицы $ mathbf H $ были различными.
Код Хэмминга
Если в сообщение включено больше исправляющих ошибок битов, и если эти биты могут быть расположены так, что разные неправильные биты дают разные результаты ошибок, то плохие биты могут быть идентифицированы. В семибитном сообщении существует семь возможных однобитовых ошибок, поэтому три бита контроля ошибок потенциально могут указывать не только на то, что произошла ошибка, но и на то, какой бит вызвал ошибку.
Хэмминг также заметил проблемы с переворачиванием двух или более битов и описал это как «расстояние» (теперь оно называется расстоянием Хэмминга, после него). Четность имеет расстояние 2, поэтому одно переключение бита можно обнаружить, но не исправить, и любые два изменения бита будут невидимы. Повторение (3,1) имеет расстояние 3, так как три бита необходимо перевернуть в одной и той же тройке, чтобы получить другое кодовое слово без видимых ошибок. Он может исправлять однобитовые ошибки или обнаруживать, но не исправлять, двухбитовые ошибки. Повторение (4,1) (каждый бит повторяется четыре раза) имеет расстояние 4, поэтому переворот трех битов можно обнаружить, но не исправить. Когда три бита в одной группе меняются местами, могут возникнуть ситуации, когда попытка исправить приведет к неправильному кодовому слову. Как правило, код с расстоянием k может обнаруживать, но не исправлять k – 1 ошибок.
Хэмминга интересовали сразу две проблемы: как можно больше увеличить расстояние и в то же время как можно больше увеличить скорость кода. В 1940-х годах он разработал несколько схем кодирования, которые значительно улучшили существующие коды. Ключом ко всем его системам было перекрытие битов четности, чтобы им удавалось проверять друг друга, а также данные.
Общий алгоритм
Следующий общий алгоритм генерирует код исправления одиночных ошибок (SEC) для любого количества битов. Основная идея состоит в том, чтобы выбрать биты с исправлением ошибок так, чтобы индекс-XOR (XOR всех битовых позиций, содержащих 1) был равен 0. Мы используем позиции 1, 10, 100 и т. Д. ( в двоичном формате) в качестве битов исправления ошибок, что гарантирует возможность установки битов исправления ошибок так, чтобы индекс-исключающее ИЛИ всего сообщения был равен 0. Если получатель получает строку с индексом-исключающее ИЛИ 0, он может заключить повреждений не было, в противном случае индекс-XOR указывает индекс поврежденного бита.
Алгоритм может быть выведен из следующего описания:
- Пронумеруйте биты, начиная с 1: бит 1, 2, 3, 4, 5, 6, 7 и т. Д.
- Запись номера битов в двоичном формате: 1, 10, 11, 100, 101, 110, 111 и т. д.
- Все позиции битов, которые являются степенями двойки (имеют один бит 1 в двоичной форме их позиции) являются битами четности: 1, 2, 4, 8 и т. д. (1, 10, 100, 1000)
- Все остальные битовые позиции, с двумя или более 1 битами в двоичной форме их позиции, являются данными биты.
- Каждый бит данных включен в уникальный набор из 2 или более битов четности, что определяется двоичной формой его битовой позиции. Бит четности 1 охватывает все битовые позиции, для которых установлен наименьший значащий бит: бит 1 (сам бит четности), 3, 5, 7, 9 и т. Д.Бит четности 2 охватывает все позиции битов, для которых установлен второй младший значащий бит: бит 2 (сам бит четности), 3, 6, 7, 10, 11 и т. Д.Бит четности 4 охватывает все позиции битов, для которых установлен третий младший значащий бит: биты 4–7, 12–15, 20–23 и т. Д.Бит четности 8 охватывает все биты позиции, в которых установлен четвертый младший значащий бит: биты 8–15, 24–31, 40–47 и т. д.Как правило, каждый бит четности охватывает все биты, для которых выполняется побитовое И позиция четности и позиция бита не равны нулю.
- Бит четности 1 охватывает все битовые позиции, для которых установлен наименьший значащий бит: бит 1 (сам бит четности), 3, 5, 7, 9 и т. Д.
- Бит четности 2 охватывает все позиции битов, для которых установлен второй младший значащий бит: бит 2 (сам бит четности), 3, 6, 7, 10, 11 и т. Д.
- Бит четности 4 охватывает все позиции битов, для которых установлен третий младший значащий бит: биты 4–7, 12–15, 20–23 и т. Д.
- Бит четности 8 охватывает все биты позиции, в которых установлен четвертый младший значащий бит: биты 8–15, 24–31, 40–47 и т. д.
- Как правило, каждый бит четности охватывает все биты, для которых выполняется побитовое И позиция четности и позиция бита не равны нулю.
Если байт данных, который должен быть закодирован, равен 10011010, то слово данных (с использованием _ для представления битов четности) будет __1_001_1010, а кодовое слово – 011100101010.
Выбор четности, четной или нечетной, не имеет значения, но один и тот же выбор должен использоваться как для кодирования, так и для декодирования.
Это общее правило можно показать визуально:
Показаны только 20 закодированных битов (5 четности, 15 данных), но шаблон продолжается бесконечно. Ключевой особенностью кодов Хэмминга, которую можно увидеть при визуальном осмотре, является то, что любой заданный бит включен в уникальный набор битов четности. Чтобы проверить наличие ошибок, проверьте все биты четности. Шаблон ошибок, называемый синдромом ошибки , определяет бит с ошибкой. Если все биты четности верны, ошибки нет. В противном случае сумма позиций ошибочных битов четности идентифицирует ошибочный бит. Например, если биты четности в позициях 1, 2 и 8 указывают на ошибку, то бит 1 + 2 + 8 = 11 является ошибочным. Если только один бит четности указывает на ошибку, сам бит четности ошибочен.
Линейные коды
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов3). Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
Теорема 1. Имеет место матричное равенство
Видим, что по структуре матрицы $ mathbf G $ и $ mathbf H $ очень похожи друг на друга. Задав одну из них, однозначно определяем другую. В одном из следующих пунктов, мы воспользуемся этим обстоятельством — для целей исправления ошибок оказывается выгоднее сначала задавать $ mathbf H $.
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
[7,4] Код Хэмминга
Графическое изображение четырех битов данных и трех битов четности и какие биты четности применяются к каким битам данных
Построение G и H
Это конструкция из G и H в стандартной (или систематической) форме. Независимо от формы, G и H для линейных блочных кодов должны удовлетворять
Таким образом, H – это матрица, левая часть которой представляет собой все ненулевые наборы из n элементов, где порядок наборов из n элементов в столбцах матрицы не имеет значения. Правая часть – это просто (n – k) – единичная матрица.
Итак, G может быть получена из H путем транспонирования левой части H с единичной k- единичной матрицей в левой части G.
Наконец, эти матрицы можно преобразовать в эквивалентные несистематические коды с помощью следующих операций:
- Перестановки столбцов (замена столбцов)
- Операции с элементарными строками (замена строки линейной комбинацией строк)
Кодирование
Коды Хэмминга имеют минимальное расстояние 3, что означает, что декодер может обнаруживать и исправлять одиночную ошибку, но не может отличить двойную битовую ошибку некоторого кодового слова от одиночной битовой ошибки другого c. одесловие. Таким образом, некоторые двухбитовые ошибки будут неправильно декодированы, как если бы они были одноразрядными ошибками, и, следовательно, останутся необнаруженными, если не будет предпринята попытка исправления.
Чтобы исправить этот недостаток, коды Хэмминга могут быть расширены дополнительным битом четности. Таким образом, можно увеличить минимальное расстояние кода Хэмминга до 4, что позволяет декодеру различать одиночные битовые ошибки и двухбитовые ошибки. Таким образом, декодер может обнаруживать и исправлять одиночную ошибку и в то же время обнаруживать (но не исправлять) двойную ошибку.
Если декодер не пытается исправить ошибки, он может надежно обнаружить тройные битовые ошибки. Если декодер исправляет ошибки, некоторые тройные ошибки будут ошибочно приняты за одиночные и «исправлены» до неправильного значения. Таким образом, исправление ошибок – это компромисс между уверенностью (способностью надежно обнаруживать тройные битовые ошибки) и отказоустойчивостью (способностью продолжать работу перед лицом однобитовых ошибок).
Этот расширенный код Хэмминга популярен в системах памяти компьютеров, где он известен как SECDED (сокращенно от «исправление одиночных ошибок», «обнаружение двойных ошибок»). Особенно популярен код (72,64), усеченный (127,120) код Хэмминга плюс дополнительный бит четности, который имеет такие же объемы служебных данных, как и код четности (9,8).
Построение кода
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
Если при передаче произошла ровно одна ошибка, то код Хэмминга способен ее исправить; если при передаче произошло ровно две ошибки, то код Хэмминга достоверно устанавливает лишь факт наличия ошибки.
Если попробовать исправить заглавие предыдущего пункта, исходя только из информации о структуре набора составляющих текст букв, то этой информации оказывается недостаточно: набор букв в правильном тексте будет таким же
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M ge 2 $.
Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,dots,b_n) $ и $ C=(c_1,dots,c_n) $ из $ mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $
ho(B,C) $.
$
ho(X_1,X_2) ge 0 $, и $
ho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
$
ho(X_1,X_2) =
ho(X_2,X_1) $;
$
ho(X_1,X_3)le
ho(X_1,X_2)+
ho(X_2,X_3) $ («неравенство треугольника»).
б) существует код $ mathbb U subset mathbb V^n $, состоящий из $ 2,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Пример. Для $ n=10 $ имеем
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
История
Ричард Хэмминг, изобретатель кодов Хэмминга, работал в Bell Labs в конце 1940-х годов над компьютером Bell Model V., электромеханическая релейная машина с временем цикла в секундах. Ввод подавался на перфоленту шириной семь восьмых дюйма, которая имела до шести отверстий в ряду. В будние дни при обнаружении ошибок в реле машина останавливалась и мигала, чтобы операторы могли исправить проблему. В нерабочее время и в выходные дни, когда не было операторов, машина просто переходила к следующему заданию.
Хэмминг работал по выходным и все больше разочаровывался в необходимости перезапускать свои программы с нуля из-за обнаруженных ошибок. В записанном на пленку интервью Хэмминг сказал: «И поэтому я сказал:« Черт побери, если машина может обнаружить ошибку, почему она не может определить местоположение ошибки и исправить ее? »». В течение следующих нескольких лет он работал над проблемой исправления ошибок, разрабатывая все более мощный набор алгоритмов. В 1950 году он опубликовал то, что теперь известно как код Хэмминга, который до сих пор используется в таких приложениях, как память ECC.
Коды, предшествующие Хэммингу
Ряд простых кодов обнаружения ошибок использовался и до Коды Хэмминга, но ни один из них не был столь же эффективен, как коды Хэмминга в том же объеме.
Четность добавляет один бит, который указывает, было ли количество единиц (битовых позиций со значением один) в предыдущих данных четным или нечетное. Если при передаче изменяется нечетное количество битов, сообщение изменит четность, и в этот момент может быть обнаружена ошибка; однако бит, который изменился, мог быть самим битом четности. Наиболее распространенное соглашение состоит в том, что значение четности, равное единице, указывает, что в данных есть нечетное количество единиц, а значение четности, равное нулю, указывает, что существует четное количество единиц. Если количество измененных битов четное, контрольный бит будет действительным и ошибка не будет обнаружена.
Более того, четность не указывает, какой бит содержит ошибку, даже если он может ее обнаружить. Данные должны быть полностью отброшены и повторно переданы с нуля. В шумной среде передачи успешная передача может занять много времени или может никогда не произойти. Однако, хотя качество проверки четности оставляет желать лучшего, поскольку он использует только один бит, этот метод дает наименьшие накладные расходы.
Код два из пяти
Код два из пяти – это схема кодирования, которая использует пять битов, состоящих ровно из трех нулей и двух единиц. Это дает десять возможных комбинаций, достаточных для представления цифр 0–9. Эта схема может обнаруживать все одиночные битовые ошибки, все битовые ошибки с нечетными номерами и некоторые битовые ошибки с четными номерами (например, переворачивание обоих 1-битов). Однако он по-прежнему не может исправить ни одну из этих ошибок.
Повторение
Другой используемый в то время код повторял каждый бит данных несколько раз, чтобы гарантировать, что он был отправлен правильно. Например, если бит данных, который должен быть отправлен, равен 1, код повторения n = 3 отправит 111. Если три полученных бита не идентичны, во время передачи произошла ошибка. Если канал достаточно чистый, большую часть времени в каждой тройке будет изменяться только один бит. Следовательно, 001, 010 и 100 соответствуют 0 биту, а 110, 101 и 011 соответствуют 1 биту, причем большее количество одинаковых цифр (‘0’ или ‘1’) указывает, что бит данных должен быть. Код с этой способностью восстанавливать исходное сообщение при наличии ошибок известен как код исправления ошибок. Этот код с тройным повторением является кодом Хэмминга с m = 2, поскольку имеется два бита четности и 2 – 2 – 1 = 1 бит данных.
Однако такие коды не могут правильно исправить все ошибки. В нашем примере, если канал переворачивает два бита и получатель получает 001, система обнаружит ошибку, но сделает вывод, что исходный бит равен 0, что неверно. Если мы увеличим размер битовой строки до четырех, мы сможем обнаружить все двухбитовые ошибки, но не сможем исправить их (количество битов четности четное); при пяти битах мы можем как обнаруживать, так и исправлять все двухбитовые ошибки, но не все трехбитные ошибки.
Более того, увеличение размера строки битов четности неэффективно, так как в нашем исходном случае пропускная способность снижается в три раза, а эффективность резко падает, когда мы увеличиваем количество дублирований каждого бита для обнаружения и исправьте больше ошибок.
