Содержание
- Код хэмминга 7 4 пример для чайников
- Код Хэмминга. Пример работы алгоритма
- Как это работает.
- Подготовка
- Вычисление контрольных бит.
- Декодирование и исправление ошибок.
- Заключение.
- Примечание.
- Код Хэмминга (7; 4)
- Найдены возможные дубликаты
- Да разве всё упомнишь
- Игрушка
- Прививки
- Реклама
- Собеседование
- Неудобно получилось
- Не happy end
- Быдло напало на девочек
- Неожиданно
- Традиции
- Pro свадьбу
Для нахождения двоичной ошибки
Для обнаружения двойной ошибки следует только добавить еще один проверочный разряд.
Пример 1:
Принята кодовая комбинация С = 101000001001, произошло искажение 2-го и 5-го разрядов. Обнаружить ошибки.
Решение.
Значения проверок равны:
k1= b1 b3 b5 b7 b9 b11 = 110010= 1
k2= b2 b3 b6 b7 b10 b11= 010000=1
k3=b4 b5 b6 b7 b12= 00001=1
k4= b8 b9 b10 b11 b12= 01001=0
Тогда контрольное число (синдром) ошибки равно 0111.
Таким образом, при наличии двукратной ошибки декодирование дает номер разряда с ошибкой в позиции 7, в то время как ошибки произошли во 2-м и 5-м разрядах. В этом случае составляется расширенный код Хэмминга, путем добавления одного проверочного символа.
Пример 2 :
Передана кодовая комбинация “01001011”, закодированная кодом Хемминга с d=4. Показать процесс выявления ошибки.
Решение:
1. Принята комбинация “01001111”:
а) проверка на общую четность указывает на наличие ошибки (число единиц четное);
б) частные проверки производятся так же, как это было в других примерах.
При составлении проверочных сумм последние единицы кодовых комбинаций (дополнительные контрольные символы) не учитываются.
2. Принята комбинация “01101111”:
а) проверка на общую четность показывает, что ошибка не фиксируется;
б) частные проверки (последний символ отбрасывается)
Первая проверка 0 1 1 1 = 1
Вторая проверка 1 1 1 1 = 0
Третья проверка 0 1 1 1 = 1
Таким образом, частные проверки фиксируют наличие ошибки. Она, якобы, имела место на пятой позиции. Но так как при этом первая проверка на общую четность ошибки не зафиксировала, то значит, имела место двойная ошибка. Исправить двойную ошибку такой код не может.
Вывод: Таким образом, мы показали, как работает код Хемминга на практике. Мы видим, что при одиночной ошибке ее можно исправить, но для этого нам нужно знать, сколько потребуется контрольных разрядов, а двойную ошибку можно лишь обнаружить.
ЗАКЛЮЧЕНИЕ
Высокие требования к достоверности передачи, обработки и хранения информации диктуют необходимость такого кодирования информации, при котором обеспечивалось бы возможность обнаружения и исправления ошибок. Широкому применению результатов теории помехоустойчивого кодирования в современных системах связи, обработки и хранения информации следует считать отсутствие достаточно простых решений сложных теоретических достижений теории помехоустойчивого кодирования.
ДОМАШНЕЕ ЗАДАНИЕ:подготовить реферат по теме «Алгоритмы обработки информации».
Ответ на домашнее задание выслать (в виде фотографий или документов Microsoft Word) на электронный адрес:
larisanikolaevna.epgl@yandex.ru
– Нарисовать структурную схему кодера и декодера, исправляющего ошибку.
– Определить проверочный код для передаваемой кодовой комбинации 1011.
– Исправить ошибку, допущенную в четвертом элементе принятой кодовой комбинации.
Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока. Поясним идею проверки на чётность на примере простейшего корректи-рующего кода, который так и называется кодом с проверкой на чётность иликодом с проверкой по паритету (равенству).В таком коде к кодовым комбинациям безизбыточного первичного двоич-ного k – разрядного кода добавляется один дополнительный разряд (символпроверки на чётность, называемый проверочным, или контрольным). Если чис-ло символов “1” исходной кодовой комбинации чётное, то в дополнительномразряде формируют контрольный символ 0, а если число символов “1” нечёт-ное, то в дополнительном разряде формируют символ 1. В результате общеечисло символов “1” в любой передаваемой кодовой комбинации всегда будет чётным.Таким образом, правило формирования проверочного символа сводится кследующему:
r1 = i1 ⊕ i2 ⊕ … ⊕ ik ,
где i – соответствующий информационный символ (0 или 1), k – общее их числоа под операцией “⊕” здесь и далее понимается сложение по mod2. Очевидно,что добавление дополнительного разряда увеличивает общее число возмож-ных комбинаций вдвое по сравнению с числом комбинаций исходного первич-ного кода, а условие чётности разделяет все комбинации на разрешённые инеразрешённые. Код с проверкой на чётность позволяет обнаруживать одиноч-ную ошибку при приёме кодовой комбинации, так как такая ошибка нарушаетусловие чётности, переводя разрешённую комбинацию в запрещённую.Критерием правильности принятой комбинации является равенство нулюрезультата S суммирования по mod 2 всех n символов кода, включая провероч-ный символ r1. При наличии одиночной ошибки S принимает значение 1:
S = r1 ⊕ i1 ⊕ i2 ⊕ . . . ⊕ ik = 0 – ошибки нет
1444424443 = 1 – однократная ошибка. n
Этот код является (k +1, k) – кодом, или (n, n -1) – кодом. Минимальное рас-стояние кода равно двум (d min = 2), и, следовательно, никакие ошибки не могутбыть исправлены. Простой код с проверкой на чётность может использоватьсятолько для обнаружения (но не исправления) однократных ошибок.Увеличивая число дополнительных проверочных разрядов и формируя поопределённым правилам проверочные символы r, равные 0 или 1, можно уси-лить корректирующие свойства кода так, чтобы он позволял не только обнару-живать, но и исправлять ошибки. На этом и основано построение кодов Хем-минга.Коды Хемминга. Рассмотрим эти коды, позволяющие исправлять одиноч-ную ошибку, с помощью непосредственного описания. Для каждого числа про-верочных символов r = 3,4,5… существует классический код Хемминга с марки-ровкой (n,k) = (2r–1, 2r–1 –r) , (3.20)
т.е. – (7,4), (15,11), (31,26) …
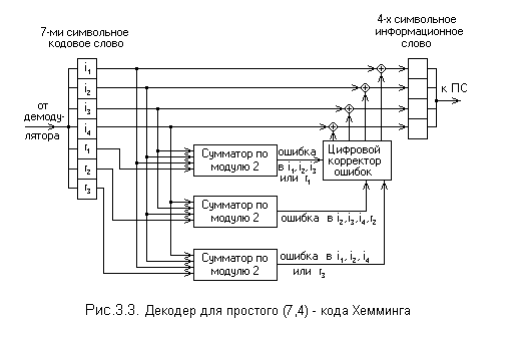
При других значениях числа информационных символов k получаются такназываемые усечённые (укороченные) коды Хемминга. Так, для международно-го телеграфного кода МТК-2 , имеющего 5 информационных символов, потре-буется использование корректирующего кода (9,5), являющегося усечённым отклассического кода Хемминга (15,11), так как число символов в этом кодеуменьшается (укорачивается) на 6. Для примера рассмотрим классический кодХемминга (7,4), который можно сформировать и описать с помощью кодера,представленного на рис.3.2. В простейшем варианте при заданных четырёх(k=4) информационных символах (i1, i2, i3, i4) будем полагать, что они сгруппиро-ваны в начале кодового слова, хотя это и не обязательно. Дополним эти ин-формационные символы тремя проверочными символами (r = 3), задавая ихследующими равенствами проверки на чётность, которые определяются соот-ветствующими алгоритмами [3,5]:
r1 = i1 ⊕ i2 ⊕ i3;
r2 = i2 ⊕ i3 ⊕ i4;
r3 = i1 ⊕ i2 ⊕ i4,
где знак ⊕ означает сложение по модулю 2.
В соответствии с этим алгоритмом определения значений проверочныхсимволов ri ниже выписаны все возможные 16 кодовых слов (7,4) – кода Хем-минга.
На рис. 3.3 приведена схема декодера для (7,4) – кода Хемминга, на входкоторого поступает кодовое слово
V = ( i1′, i2′, i3′, i4′, r1′, r2′, r3′)
Апостроф означает, что любой символ слова может быть искажён помехой вканале передачи.
В декодере в режиме исправления ошибок строится последовательность:
s1 = r1′ ⊕ i1′ ⊕ i2′ ⊕ i3′;
s2 = r2′ ⊕ i2′ ⊕ i3′ ⊕ i4′;
s3 = r3′ ⊕ i1′ ⊕ i2′ ⊕ i4′. Трёхсимвольная последовательность ( s1, s2, s3 ) называется синдромом.
Термин “синдром” используется и в медицине, где он обозначает сочетаниепризнаков, характерных для определённого заболевания. В данном случаесиндром S = (s1, s2, s3 ) представляет собой сочетание результатов проверкина чётность соответствующих символов кодовой группы и характеризует опре-делённую конфигурацию ошибок (шумовой вектор).
Кодовые слова (7,4) – кода Хемминга.
к = 4 r = 3
i1 i2 i3 i4 r1 r2 r3
0 0 0 0 0 0 0
0 0 0 1 0 1 1
0 0 1 0 1 1 0
0 0 1 1 1 0 1
0 1 0 0 1 1 1
0 1 0 1 1 0 0
0 1 1 0 0 0 1
0 1 1 1 0 1 0
1 0 0 0 1 0 1
1 0 0 1 1 1 0
1 0 1 0 0 1 1
1 0 1 1 0 0 0
1 1 0 0 0 1 0
1 1 0 1 0 0 1
1 1 1 0 1 0 0
1 1 1 0 1 1 1
Число возможных синдромов определяется выражением S = 2r. (3.21)
При числе проверочных символов r = 3 имеется восемь возможных син-дромов (23 = 8). Нулевой синдром (000) указывает на то, что ошибки при приёмеотсутствуют или не обнаружены. Всякому ненулевому синдрому соответствуетопределённая конфигурация ошибок, которая и исправляется. Классическиекоды Хемминга (3.20) имеют число синдромов, точно равное их необходимомучислу, позволяют исправить все однократные ошибки в любом информативноми проверочном символах и включают один нулевой синдром. Такие коды назы-ваются плотноупакованными.Усечённые коды являются неплотноупакованными, так как число синдро-мов у них превышает необходимое. Так, в коде (9,5) при четырёх проверочныхсимволах число синдромов будет равно 24 =16, в то время как необходимо все-го 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5).
Для рассматриваемого кода (7,4) в таблице 1 представлены ненулевыесиндромы и соответствующие конфигурации ошибок.
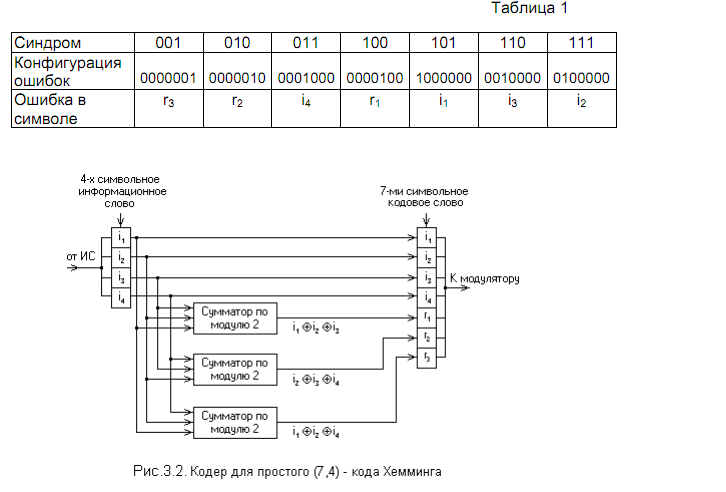
Таким образом, код (7,4) позволяет исправить все одиночные ошибки.Простая проверка показывает, что каждая из ошибок имеет свой единственныйсиндром. При этом возможно создание такого цифрового корректора ошибок(дешифратора синдрома), который по соответствующему синдрому исправляетсоответствующий символ в принятой кодовой группе. После внесения исправ-ления проверочные символы ri можно на выход декодера (рис.3.3) не выводить.Две или более ошибки превышают возможности корректирующего кода Хем-минга, и декодер будет ошибаться. Это означает, что он будет вносить не-правильные исправления и выдавать искажённые информационные символы.Идея построения подобного корректирующего кода, естественно, не меня-ется при перестановке позиций символов в кодовых словах. Все такие вариан-ты также называются (7,4) – кодами Хемминга
Код Хэмминга (7,4) восходит к 1950 году. В то время Ричард Хэмминг работал математиком в Bell Labs. Каждую пятницу Хэмминг настраивал вычислительные машины на выполнение серии расчетов и собирал результаты в следующий понедельник. Используя проверки на четность, эти машины смогли обнаружить ошибки во время вычислений. Разочарованный, потому что он получал сообщения об ошибках слишком часто, Хэмминг решил улучшить обнаружение ошибок и обнаружил известные коды Хемминга.
Механика Хэмминга (7,4)
Цель кодов Хэмминга состоит в том, чтобы создать набор битов четности, которые перекрываются так, что однобитовая ошибка (один бит переворачивается) в бите данных или бит четности может быть обнаружена и исправлена. Только в случае множественных ошибок код Хэмминга не может восстановить исходные данные. Он может вообще не заметить ошибку или даже исправить ее неверно. Поэтому в этой задаче мы будем иметь дело только с однобитовыми ошибками.
В качестве примера кодов Хэмминга мы рассмотрим код Хемминга (7,4). В дополнение к 4 битам данных d1, d2, d3, d4используются 3 бита четности p1, p2, p3, которые рассчитываются с использованием следующих уравнений:
p1 = (d1 + d2 + d4) % 2
p2 = (d1 + d3 + d4) % 2
p3 = (d2 + d3 + d4) % 2
Результирующее кодовое слово (данные + биты четности) имеет вид p1 p2 d1 p3 d2 d3 d4.
Обнаружение ошибки работает следующим образом. Вы пересчитываете биты четности и проверяете, соответствуют ли они принятым битам четности. В следующей таблице вы можете видеть, что каждое разнообразие однобитовой ошибки приводит к различному соответствию битов четности. Следовательно, каждая однобитовая ошибка может быть локализована и исправлена.
error in bit | p1 | p2 | d1 | p3 | d2 | d3 | d4 | no error
-------------|---------------------------------------------
p1 matches | no | yes| no | yes| no | yes| no | yes
p2 matches | yes| no | no | yes| yes| no | no | yes
p3 matches | yes| yes| yes| no | no | no | no | yes
пример
Пусть ваши данные будут 1011. Биты четности есть p1 = 1 + 0 + 1 = 0, p2 = 1 + 1 + 1 = 1и p3 = 0 + 1 + 1 = 0. Объедините данные и биты четности, и вы получите кодовое слово 0110011.
data bits | 1 011
parity bits | 01 0
--------------------
codeword | 0110011
Скажем, во время передачи или вычисления 6-й бит (= 3-й бит данных) переворачивается. Вы получаете слово 0110001. Предполагаемые полученные данные есть 1001. Вы снова вычислить биты четности p1 = 1 + 0 + 1 = 0, p2 = 1 + 0 + 1 = 0, p3 = 0 + 0 + 1 = 1. Соответствует только p1битам четности кодового слова 0110001. Поэтому произошла ошибка. Глядя на таблицу выше, говорит нам, что произошла ошибка, d3и вы можете восстановить исходные данные 1011.
Вызов:
Это код-гольф. Поэтому самый короткий код выигрывает.
Тестовые случаи:
1110000 -> 1000 # no error
1100000 -> 1000 # error at 1st data bit
1111011 -> 1111 # error at 2nd data bit
0110001 -> 1011 # error at 3rd data bit (example)
1011011 -> 1010 # error at 4th data bit
0101001 -> 0001 # error at 1st parity bit
1010000 -> 1000 # error at 2nd parity bit
0100010 -> 0010 # error at 3rd parity bit
Ответы:
Октава, 70 66 55 байт
Эта функция Fустанавливает матрицу декодирования H, находит ошибку и корректирует ее положение (если оно есть). Затем он возвращает правильные биты данных. Ввод является стандартным вектором строки.
F=@(c)xor(c,1:7==bi2de(mod(c*de2bi(1:7,3),2)))([3,5:7])
Ниже приводится самое короткое решение в Matlab , так как вы не можете напрямую использовать индексирование для выражений. (Это работает и в Octave, конечно.) Был в состоянии заменить дополнение / mod2 на xor:
f=@(c)c([3,5:7]);F=@(c)f(xor(c,1:7==bi2de(mod(c*de2bi(1:7,3),2))))
f=@(c)c([3,5:7]);F=@(c)f(mod(c+(1:7==bi2de(mod(c*de2bi(1:7,3),2))),2))
Пит 50х11 = 550

Размер кода равен 15. Не слишком обеспокоен размером, но он прошел все тесты.
Python, 79
Возьмите ввод и вывод как числа с младшим значащим битом справа.
Вместо того, чтобы пытаться исправить ошибки, мы просто пытаемся кодировать каждое возможное сообщение nот 0 до 15, пока не получим кодировку, которая находится на расстоянии одного бита от того, что дано. Рекурсия продолжает увеличиваться, nпока не найдет тот, который работает, и не вернет его. Хотя явного завершения нет, оно должно заканчиваться в 16 циклах.
Выражение (n&8)*14^(n&4)*19^(n&2)*21^n%2*105реализует битовую матрицу Хемминга.
Чтобы проверить наличие одной ошибки, мы зашифровываем данное сообщение с вычисленным значением eи проверяем, является ли оно степенью двойки (или 0) с помощью классического бит-трюка e&~-e==0. Но на самом деле мы не можем присвоить переменную eв лямбде, и мы ссылаемся на нее дважды в этом выражении, поэтому мы делаем хак, передавая ее в качестве необязательного аргумента следующему рекурсивному шагу.
JavaScript (ES6), 92 87 81
- calc p3wrong | p2wrong | p1wrong (строка 2,3,4)
- используйте его как битовую маску, чтобы перевернуть неправильный бит (строка 1),
- затем вернуть только биты данных (последняя строка)
Тест в консоли Frefox / FireBug
;[0b1110000,0b1100000,0b1111011,0b0110001,
0b1011011,0b0101001,0b1010000,0b0100010]
.map(x=>x.toString(2)+'->'+F(x).toString(2))
["1110000->1000", "1100000->1000", "1111011->1111", "110001->1011", "1011011->1010", "101001->1", "1010000->1000", "100010->10"]
Python 2, 71
f=lambda i,b=3:i&7|i/2&8if chr(i)in'\0%*3<CLUZfip'else f(i^b/2,b*2)
Несколько символов являются непечатаемыми ASCII, поэтому здесь есть экранированная версия:
f=lambda i,b=3:i&7|i/2&8if chr(i)in'\0\x0f\x16\x19%*3<CLUZfip\x7f'else f(i^b/2,b*2)
Вход и выход в функцию выполняются как целые числа.
Я пользуюсь тем фактом, что количество действительных сообщений составляет всего 16, и жестко их всех кодирую. Затем я пытаюсь переворачивать разные биты, пока не получу один из них.
Haskell, 152 байта
a(p,q,d,r,e,f,g)=b$(d+e)#p+2*(d+f)#q+4*(e+f)#r where b 3=(1-d,e,f,g);b 5=(d,1-e,f,g);b 6=(d,e,1-f,g);b 7=(d,e,f,g-1);b _=(d,e,f,g);x#y=abs$(x+g)`mod`2-y
Использование: a (1,1,1,1,0,1,1)какие выводы(1,1,1,1)
Простое решение: если pне совпадает, установите бит в число. Если это число 3, 5, 6или 7, флип соответствующий d.
Машинный код IA-32, 36 байтов
33 c0 40 91 a8 55 7a 02 d0 e1 a8 66 7a 03 c0 e1
02 a8 78 7a 03 c1 e1 04 d0 e9 32 c1 24 74 04 04
c0 e8 03 c3
Эквивалентный код C:
unsigned parity(unsigned x)
{
if (x == 0)
return 0;
else
return x & 1 ^ parity(x >> 1);
}
unsigned fix(unsigned x)
{
unsigned e1, e2, e3, err_pos, data;
e1 = parity(x & 0x55);
e2 = parity(x & 0x66);
e3 = parity(x & 0x78);
err_pos = e1 + e2 * 2 + e3 * 4;
x ^= 1 << err_pos >> 1;
data = x;
data &= 0x74;
data += 4;
data >>= 3;
return data;
}
Процессор x86 автоматически вычисляет четность каждого промежуточного результата. Он имеет специальную инструкцию, jpкоторая прыгает или не прыгает в зависимости от четности.
Это не было указано явно в вызове, но удобное свойство кодов Хэмминга заключается в том, что вы можете интерпретировать биты четности как двоичное число, и это число указывает, какой бит был испорчен во время передачи. На самом деле это число основано на 1, причем 0 означает, что ошибок передачи не было. Это реализуется путем смещения 1 влево, err_posа затем вправо 1.
После исправления ошибки передачи код размещает биты данных в нужном порядке. Код оптимизирован по размеру, и поначалу может быть неясно, как он работает. Чтобы объяснить это, я обозначу через a, b, c, dбиты данных, и P, Qи Rбиты четности. Потом:
data = x; // d c b R a Q P
data &= 0x74; // d c b 0 a 0 0
data += 4; // d c b a ~a 0 0
data >>= 3; // d c b a
Источник сборки (fastcall соглашение, с входом ecxи выходом eax):
xor eax, eax;
inc eax;
xchg eax, ecx;
test al, 0x55;
jp skip1;
shl cl, 1;
skip1:
test al, 0x66;
jp skip2;
shl cl, 2;
skip2:
test al, 0x78;
jp skip3;
shl ecx, 4;
skip3:
shr cl, 1;
xor al, cl;
and al, 0x74;
add al, 4;
shr al, 3;
ret;
Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H(n,k), имеющей строк и столбцов, причем столбцами H(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до ).
Длина кодовой комбинации кода Хэмминга равна .
Число информационных элементов определяется как .
Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.
Зная вид матрицы H(n,k), можно определить корректирующие свойства (n, k) – кода Хэмминга. Так как все столбцы матрицы проверок различны, то никакие два столбца H(n,k) не являются линейно зависимыми. Наряду с этим, для любого числа m всегда можно указать три столбца матрицы H(n,k), которые линейно зависимы, например, столбцы, соответствующие числам 1, 2, 3. Следовательно, для любого (n, k) – кода Хэмминга dmin=3.
Код Хэмминга является одним из немногочисленных примеров совершенного кода.
Действительно, поскольку (n, k) – код Хэмминга исправляет все одиночные ошибки, то все образцы одиночных ошибок (а их всего насчитывается вариантов) должны разместиться в различных смежных классах, число которых также равно . Следовательно, помимо смежных классов, содержащих образцы одиночных ошибок, никаких других в таблице декодирования не имеется, что и подтверждает совершенность кода Хэмминга.
При фиксированном числе можно построить код Хэмминга любой длины () путем укорочения (n, k) – кода. Укорочение не уменьшает минимальное кодовое расстояние. В силу того, что для любого числа n существует код Хэмминга, любой групповой код с исправлением одиночных ошибок принято называть кодом Хэмминга.
Пример 5.13. Определим параметры кодов Хэмминга естественной длины для различных значений m. Результаты представим в виде таблицы.
| m | 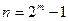
|
k | 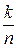
|
| 0,33 | |||
| 0,57 | |||
| 0,74 | |||
| 0,84 | |||
| 0,91 | |||
| 0,95 |
и т.д.
Очевидно, что минимальная длина кода Хэмминга, имеющего практическое значение, есть 3. При увеличении n отношение возрастает и стремится к 1.
Пример 5.14. Рассмотрим код Хэмминга (7,4). Матрица проверок этого кода состоит из 7 трехразрядных двоичных чисел от 1 до 7:
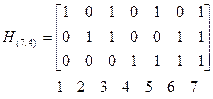 .
.
Из рассмотрения этой матрицы видно, что минимальное число линейно зависимых столбцов равно 3( к примеру 1, 2 и 3), следовательно, dmin=3.
В том случае, когда столбцы матрицы H(n,k) – кода Хэмминга есть упорядоченная запись m – разрядных двоичных чисел, декодирование осуществляется оригинальным образом. В результате вычисления проверочного соотношения для кодовой комбинации , имеющей одиночную ошибку, получается синдром в точности равный номеру элемента, в котором произошла ошибка.
Действительно, если ei содержит одну единицу в разряде, соответствующем ошибочному элементу, то при умножении на матрицу НТ все строки матрицы НТ, соответствующие нулям в ei, обращаются в нули, и лишь строка, соответствующая “1” в ei сохраняет свой вид (т.е. порядковый номер элемента в двоичной записи) в ответе.
Пример 5.15. Пусть приемник УЗО системы передачи данных зарегистрировал комбинацию . Вычисление синдрома дает
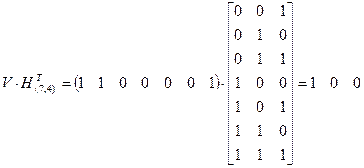 ,
,
т.е. ошибка в четвертом элементе и кодовая комбинация кода (7,4), которая была передана, имеет вид:
Путем несложных преобразований из (n, k) – кода Хэмминга с dmin=3 можно получить (n+1, k) – код Хэмминга с dmin=4.
Для этого в кодовую комбинацию вводится избыточный элемент, являющийся результатом проверки на четность по всем элементам кодовой комбинации. Число информационных элементов остается прежним.
Матрица проверок для (n+1, k) – кода Хэмминга с dmin=4 получается из матрицы проверок (n, k) – кода с dmin=3 путем введения дополнительной строки из (n+1)-ой единицы.
Так как размерность матрицы проверок кода с dmin=4 должна быть равна , то к каждой строке матрицы проверок кода с dmin=3, необходимо добавить один нулевой элемент для того, чтобы не нарушить введенные ранее проверки. Матрица проверок для (n+1, k) – кода dmin=4 имеет вид:
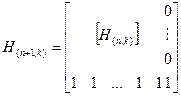 ,
,
где H(n,k) = матрица проверок исходного кода с dmin=3.
Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.
Пример 5.16. Построить код Хэмминга (8,4) с dmin=4 на основе матрицы проверок кода (7,4).
Известно:
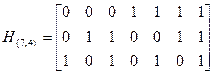
По виду матрицы можно сделать вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на четность.
Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.
Таким образом, матрице соответствует следующая система проверочных соотношений:
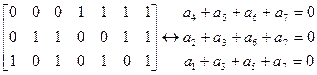
Для того, чтобы получить код (8,4) с dmin=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:
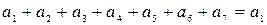
или
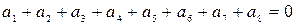 .
.
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:
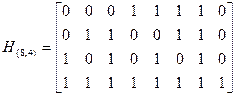 .
.
Определим известным способом dmin (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) dmin=4.
До сих пор мы еще не разделили элементы кодовой комбинации на информационные и проверочные. Наиболее рационально, по-видимому, это можно сделать следующим образом. Желательно, чтобы каждое проверочное соотношение однозначно определяло проверочный элемент как результат проверки на четность некоторой совокупности информационных элементов. В таком случае мы получили бы возможность определять значение проверочного элемента наиболее простым образом – решением одного линейного уравнения с одним неизвестным. Для этого при упорядоченной записи столбцов матрицы H(n,k) в качестве проверочных элементов необходимо брать элементы с номерами 2i, где i изменяется от 0 до m-1, так как именно эти столбцы содержат только по одной единице. Последнее свидетельствует о том, что элементы с номерами 2i входят только в одну проверку и, следовательно, они могут быть взяты в качестве проверочных.
Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).
По виду матрицы , приведенной в предыдущем примере, в качестве проверочных элементов выбираем элементы, которым соответствуют столбцы, содержащие только по одной единице, т.е. первый, второй и четвертый. Следовательно, 4 информационных элемента кода (7,4) должны занимать места 3, 5, 6 и 7-го разрядов. Приведенная в предыдущем примере система проверочных соотношений позволяет определить значение каждого из проверочных элементов по значениям информационных элементов, т.е. по значению элементов простого кода, который необходимо закодировать кодом Хэмминга
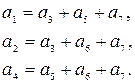
Зная места проверочных элементов, легко привести матрицу H(n,k) кода Хэмминга к канонической форме.
Для этого необходимо столбцы с номерами 2i, где при упорядоченной записи столбцов переместить на места m первых столбцов в порядке убывания номеров. В общем виде такая перестановка столбцов в матрице H(n,k) приводит к эквивалентному (n, k) – коду. В случае же кодов Хэмминга естественной длины код получается даже не эквивалентный, а в точности совпадающий с исходным кодом.
Пример 5.18. Преобразовать матрицу к канонической форме.
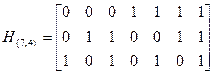
Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:
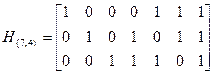 .
.
Это и есть каноническая форма матрицы . Сравнение ее с исходной матрицей показывает, что местам информационных элементов в канонической форме соответствуют столбцы с номерами 3, 5, 6, 7, а местам проверочных элементов – столбцы 4, 2, 1.
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:
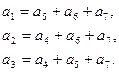
Порождающую матрицу G(n, k) для кода Хэмминга можно получить из матрицы H(n,k), используя теорему 5.3:
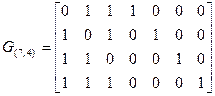
Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.
Оценим эффективность кодов Хэмминга.
а) Коды Хэмминга с dmin=3
Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратности S=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:
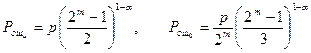 .
.
Выигрыш по достоверности по сравнению с простыми кодами той же длины составляет:
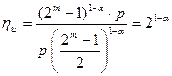
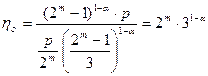
б) Коды Хэмминга с dmin=4.
Для таких кодов возможны два режима – исправление однократных ошибок и обнаружение ошибок и только обнаружение ошибок. Вероятность ошибки для этих режимов в случае группирования ошибок равна:
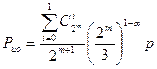
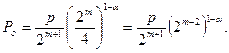
Выигрыш по достоверности по сравнению с простым кодом той же длины составляет:
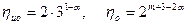 .
.
5.4.3Итеративные коды.
На основе (n, n-1) – кодов с dmin=2 или кодов Хэмминга с dmin=3 и dmin=4 можно построить коды с более высокими корректирующими свойствами. Для этой цели, наряду с защитой каждой передаваемой комбинации описанным выше способом, осуществляют помехоустойчивое кодирование одноименных разрядов групп передаваемых комбинаций. Процесс кодирования можно пояснить при помощи рис. 5.6.
Комбинации простого кода, подлежащие передаче по системе связи, записываются в виде таблицы – каждая комбинация составляет отдельную строку этой таблицы (информационные символы). Затем осуществляется кодирование по строкам и столбцам. В общем случае для кодирования строк и кодирования столбцов можно использовать различные коды. Избыточные элементы дописываются к каждой строке (проверка по строкам) и к каждому столбцу (проверка по столбцам). Проверка проверок осуществляется кодированием столбцов, составленных из избыточных элементов строк или кодированием строк, составленных из проверок столбцов. Последующее введение избыточности осуществляется для защиты блоков информации, представленных на рис. 5.6. Процесс кодирования поясняется на рис. 5.7. Из блоков информации, защищенных двумя проверками, составляется параллелепипед. Избыточные разряды третьей проверки образуют параллелепипед, выделенный утолщенной линией.
5 эл. комбинация
Рис.5.6.
 |
 |
|||||||
 |
 |
||||||
 |
|||||||
В результате итеративного кодирования получаются групповые коды, которые обладают следующим важным свойством.
Теорема 5.3. Минимальное кодовое расстояние итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.
Действительно, если в случае двух проверок минимальный вес одного кода равен , а другого , то вектор итеративного кода имеет, по крайней мере, единиц в каждой строке и элементов в каждом столбце и, следовательно, не менее единиц.
Аналогичные рассуждения можно продолжить и на случай большего числа проверок.
Порождающая матрица итеративного кода может быть построена следующим образом.
Пусть GA – порождающая матрица кода, используемого для проверки по строкам, а GВ – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (GAВ) имеет вид:
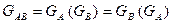 .
.
Запись означает, что на местах “1” в матрице GA записывается матрица GВ, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам GВ. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то
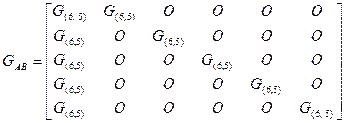 ,
,
где
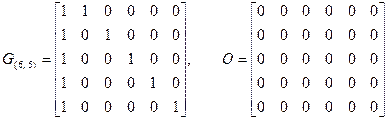 .
.
Код хэмминга 7 4 пример для чайников
Код Хэ́мминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построен применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную.
Предположим, что нужно сгенерировать код Хемминга для некоторого информационного кодового слова. В качестве примера возьмём 15-битовое кодовое слово x1…x15, хотя алгоритм пригоден для кодовых слов любой длины. В приведённой ниже таблице в первой строке даны номера позиций в кодовом слове, во второй — условное обозначение битов, в третьей — значения битов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Вставим в информационное слово контрольные биты r0…r4 таким образом, чтобы номера их позиций представляли собой целые степени двойки: 1, 2, 4, 8, 16… Получим 20-разрядное слово с 15 информационными и 5 контрольными битами. Первоначально контрольные биты устанавливаем равными нулю. На рисунке контрольные биты выделены розовым цветом.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
В общем случае количество контрольных бит в кодовом слове равно двоичному логарифму числа, на единицу большего, чем количество бит кодового слова (включая контрольные биты); логарифм округляется в большую сторону. Например, информационное слово длиной 1 бит требует двух контрольных разрядов, 2-, 3- или 4-битовое информационное слово — трёх, 5…11-битовое — четырёх, 12…26-битовое — пяти и т. д.
Добавим к таблице 5 строк (по количеству контрольных битов), в которые поместим матрицу преобразования. Каждая строка будет соответствовать одному контрольному биту (нулевой контрольный бит — верхняя строка, четвёртый — нижняя), каждый столбец — одному биту кодируемого слова. В каждом столбце матрицы преобразования поместим двоичный номер этого столбца, причём порядок следования битов будет обратный — младший бит расположим в верхней строке, старший — в нижней. Например, в третьем столбце матрицы будут стоять числа 11000, что соответствует двоичной записи числа три: 00011.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
В правой части таблицы мы оставили пустым один столбец, в который поместим результаты вычислений контрольных битов. Вычисление контрольных битов производим следующим образом. Берём одну из строк матрицы преобразования (например, r0) и находим её скалярное произведение с кодовым словом, то есть перемножаем соответствующие биты обеих строк и находим сумму произведений. Если сумма получилась больше единицы, находим остаток от его деления на 2. Иными словами, мы подсчитываем сколько раз в кодовом слове и соответствующей строке матрицы в одинаковых позициях стоят единицы и берём это число по модулю 2.
Если описывать этот процесс в терминах матричной алгебры, то операция представляет собой перемножение матрицы преобразования на матрицу-столбец кодового слова, в результате чего получается матрица-столбец контрольных разрядов, которые нужно взять по модулю 2.
Например, для строки r0:
r0 = (1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·1+0·1+1·1+0·0+1·0+0·0+1·0+0·1) mod 2 = 5 mod 2 = 1.
Полученные контрольные биты вставляем в кодовое слово вместо стоявших там ранее нулей. По аналогии находим проверочные биты в остальных строках. Кодирование по Хэммингу завершено. Полученное кодовое слово — 11110010001011110001.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Алгоритм декодирования по Хэммингу абсолютно идентичен алгоритму кодирования. Матрица преобразования соответствующей размерности умножается на матрицу-столбец кодового слова и каждый элемент полученной матрицы-столбца берётся по модулю 2. Полученная матрица-столбец получила название «матрица синдромов». Легко проверить, что кодовое слово, сформированное в соответствии с алгоритмом, описанным в предыдущем разделе, всегда даёт нулевую матрицу синдромов.
Матрица синдромов становится ненулевой, если в результате ошибки (например, при передаче слова по линии связи с шумами) один из битов исходного слова изменил своё значение. Предположим для примера, что в кодовом слове, полученном в предыдущем разделе, шестой бит изменил своё значение с нуля на единицу (на рисунке обозначено красным цветом). Тогда получим следующую матрицу синдромов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r0 | r1 | x1 | r2 | x2 | x3 | x4 | r3 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | r4 | x12 | x13 | x14 | x15 | ||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | s0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | s1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | s2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | s3 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | s4 | 0 |
Заметим, что при однократной ошибке матрица синдромов всегда представляет собой двоичную запись (младший разряд в верхней строке) номера позиции, в которой произошла ошибка. В приведённом примере матрица синдромов (01100) соответствует двоичному числу 00110 или десятичному 6, откуда следует, что ошибка произошла в шестом бите.
Источник
Код Хэмминга. Пример работы алгоритма
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части. Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:
Стало:
Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее: Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант). Высчитав контрольные биты для нашего информационного слова получаем следующее: и для второй части:
Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно): Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину: Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источник
Код Хэмминга (7; 4)
Структурно слова кода Хэмминга состоят из двух частей. Сначала идут информационные 4 бита, затем три бита проверочных. Будем обозначать информационные биты буквами ABCD, проверочные буквами xyz.
Таким образом слово кода Хэмминга имеет следующую структуру:
Для передачи 4 бит информации нам требуется передавать кодовое слово из целых 7 бит! Последние три бита в случае, когда ошибки отсутствуют, не несут никакой новой информации, ибо они зависят от первых 4. Однако если в кодовом слове из 7 бит произошла 1 ошибка, то исходные информационные 4 бита всё равно можно будет восстановить точно! В этом и состоит главная особенность самокорректирующихся кодов.
Для подсчёта проверочных бит можно использовать следующие формулы:
где n mod 2 означает остаток от деления числа n на 2.
К примеру, если информационный вектор есть ABCD = 1001, то кодовый вектор будет ABCDxyz = 1001 100
Вместо непонятных формул можно использовать следующую картинку:
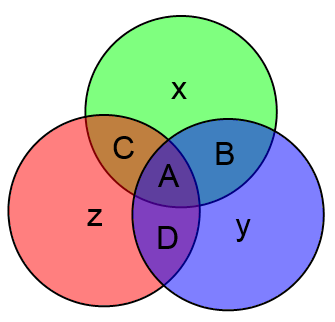
Здесь всё очень просто. Подставляете вместо букв значения соответствующих битов и затем считаете значения x, y и z как сумму по модулю 2 тех информационных бит, которые есть в соответствующем круге.
В приведённом выше примере будет:
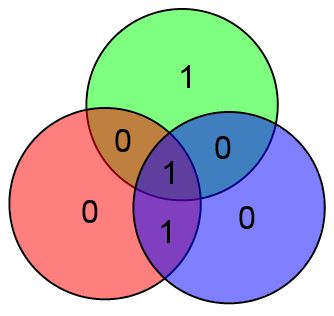
Куда более интересным является вопрос об исправлении ошибок. Очевидно, вывод об отсутствии ошибок приёмник может сделать просто взяв информационные биты ABCD, посчитав на их основе проверочные биты xyz и сравнить посчитанные проверочные биты с принятыми. Если есть ошибка, то часть проверочных битов не совпадёт.
Предположим что произошла ошибка в проверочном бите y и было принято слово 1001 110
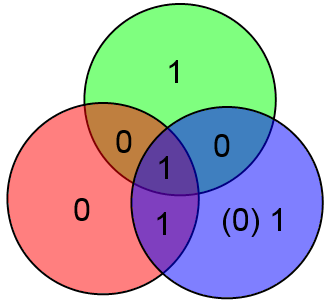
В таком случае два проверочных бита сойдутся, а один нет. Этого вполне достаточно чтобы сделать вывод что нужно исправить бит y (для которого проверка не сошлась).
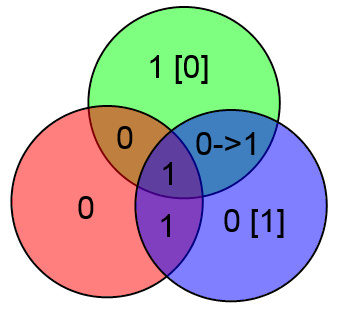
Наконец, отдельно рассмотрим бит A. Если в нём ошибка, то у нас не сойдутся все три проверки:
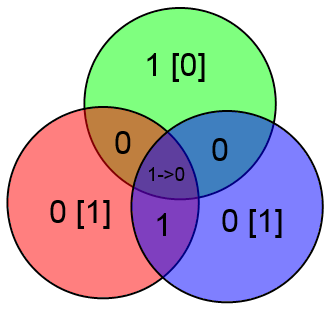
Увидев такое безобразие сразу же делаем вывод о том, что ошибка в бите A.
Таким образом, можно легко и просто вычислять локацию ошибки и исправлять её. Замечу что если ошибок больше одной, то описанный выше алгоритм сработает неверно. К примеру, допустим что произошли ошибки в битах C и z:
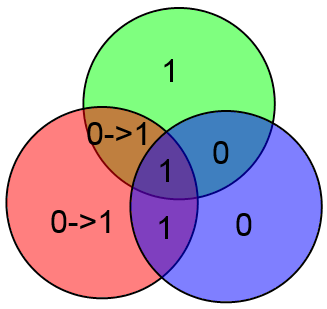
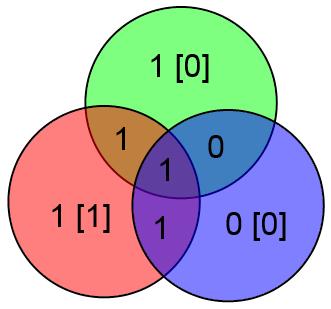
Проверочные биты y и z сойдутся, а бит x нет. Алгоритм исправит бит x и всё. Это вполне естественное поведение, т.к. если вероятность ошибки p 0).
Естественно, работать с цветными кругами удобно человеку, но неудобно компьютеру. У кодов Хэмминга есть одна особенность, которая позволяет их лёгкое декодирование на компьютере. Итак, рассмотрим следующий алгоритм:
Определим числа g, b, r как сумму всех четырёх бит в кругах соответствующего цвета. Т.е.:
g = A + B + C + x mod 2,
b = A + B + D + y mod 2,
r = A + C + D + z mod 2.
Фактически каждый из этих бит можно определить как сумму соответствующего проверочного бита, вычисленного на основании принятых информационных бит, с принятым проверочным битом. Т.е. к примеру g есть сумма (A + B + C mod 2) (по этой формуле считался x на стороне передатчика) и принятого x. Аналогично b соответствует y, r соответствует z.
Если ошибок нет, то gbr = 000 (принятые проверочные биты сошлись с вычисленными на основе информационного вектора).
Если же есть 1 ошибка, то число gbr есть номер (в двоичной записи) ошибочного бита в векторе ABCxDyz.
В качестве примера рассмотрим уже знакомый нам вектор ABCDxyz = 1001 100, в котором произошла ошибка в бите x (четвёртый бит в векторе ABCxDyz). Посчитаем gbr:
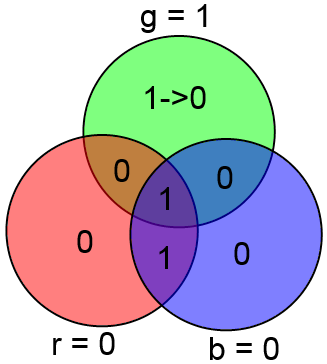
gbr = 100 [2] = 4 [10]. Ошибка в 4 бите, которым и является x. Таким образом, для декодирования и исправления ошибки в кодовом слове длины 7 требуется лишь вычислить три суммы и из полученного числа несложной функцией получить местонахождение ошибки.
На этом всё, спасибо за внимание!
Найдены возможные дубликаты
Сижу, раскуриваю коды Гоппы, и понимаю, какой милый и хороший был хэмминг 🙂
Спасибо огромное! Жаль нельзя поставить плюс(
спасибо, милый человек. благодаря посту лабу сделали xD
Нахрена мне знать об этом? т.е. какой профит? где оно надо?
Не нравится не читай. А мне было полезно.
Запоздалое спасибо. Пикабу образовательный 🙂
мне было интересно, но что дальше?

Быдло напало на девочек
Вчера 03.10.2021 примерно в 16:50 этот биомусор напал на 2-х абсолютно невинных девочек, которые возвращались домой с прогулки. Девочка в розовой курточке, это дочка моей знакомой. Девочкам по 11 лет.
На видео слышно, как он им угрожает, пытается подпалить зажигалкой и наносит несколько ударов по голове обеим девочкам, после чего скрывается.
У обоих девочек остались следы от ударов, для детей его удары оказались достаточно сильные.
Как выяснилось позже, данный индивид вышел на улицу разбираться с обидчицами его собственной дочери, но так как он не знал как они выглядят, то напал на первых попавшихся ни в чём не повинных детей.
Ещё более мерзко то, что его дочь является их одноклассницей и девочки всегда с ним здоровались, но это ни как не остановило его.
В данный момент написано заявление у инспектора по делам несовершеннолетних, планируется так же написать заявление в МВД по факту нападения на детей.
П.С. Этот человек ранее уже был судим за убийство, у него четверо детей, живёт он в соседнем подъезде и о камере в домофоне прекрасно знает.
Pro свадьбу
Прочитал пост про свадьбу и комменты, про конкурсы, про тамадов, про чудных гостей.
Я вот на свадьбах редко бывал, ну так особо не приглашали почему-то, может город маленький, может кто оклеветал. На одной правда был, запомнилось.
Приехал я сразу в кафе, чего я в том Загсе не видел, ну расселись все, подарки, тосты, поздравления и вот такой тамундак и вёл, а давайте за молодых, за гостей, за гусей, за Варлей, музей и прочее прочее, все филонили кто как мог, кто воду пил, кто сок, а я честно в силу неопытности пил за все подряд, даже если тоста ещё небыло.
В определённый момент наступил апогей апофеоза, мне стало скучно, все пустились в пляс, плясать я не умею и я пошёл на улицу, а там фонтан, нет в ВДВ я не служил, даже в ВМФ не служил, но мне захотелось в водичку. Я человек крайне воспитанный и культурный взял стул с веранды, стол, затащил это все в фонтан пока все плясали я сварганил себе закуски, выпивки и сидел интилегентно выпивал и закусывал. Меня искали, меня нашли. Вся свадьба во главе с новобрачными водили хороводы вокруг фонтана умоляя меня вернуться на берег, я был категорически против, все ржали, жена плакала, оператор снимал на видео. Потом мне стало жаль жену, я её любил и я вернулся в зал к людям. Там были конкурсы, я захотел в них быть и на каждый вопрос «кто?» я с готовностью говорил» Я». Конкурсы были разные я был и конём Князя Владимира и балериной и валютной проституткой, я читал стихи, в лицах, ролях, меня уже никто об этом не просил, тамада слился в тихом ахере от происходящего, все буквально валялись под столами, жена плакала, но во мне проснулся давно мертвый актёр и Остапа было не остановить. Я придумывал сам конкурсы, сам же в них один за всех и участвовал, я пел, танцевал, искрометно шутил, потом темнота, утро телефон разрывается. Звонил жених, потом невеста, потом их родители и какие-то совершенно чужие голоса и номера, у них мол второй день, природа, шашлыки, но никто никуда не хочет ехать без меня.
Я поехал конечно, со мной здоровались незнакомые люди, целовали незнакомые женщины, обнимали и хлопали по спине незнакомые мужчины, а незнакомые дети лезли мне на руки, все смеялись, улыбались и говорили «ну ты блин даёшь конечно», день был долгий, все смеялись, жена плакала.
Касету я с той свадьбы так ни разу и не посмотрел, сколько не уговаривали, они её дома вместо «С легким паром» на НГ смотрят, всей семьёй. Я ухожу на кухню, пусть сами ржут.
P. S. В оправдание. Мне было 23 года, я был юн и неопытен.
Источник
